查看数据源：5930b1b9802023000a9968df
在等腰 $\triangle ABC$ 中．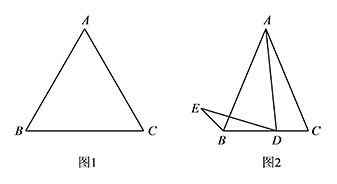
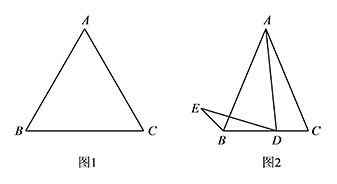
【难度】
【出处】
无
【标注】
  • 题型
    >
    几何部分
    >
    几何模型
    >
    共顶点模型
  • 题型
    >
    几何部分
    >
    几何模型
    >
    共顶点模型
  1. 若 $\triangle ABC$ 为等边三角形，点 $D$ 为线段 $BC$ 上一动点（不与 $B,C$ 重合），连接 $AD$ 并将线段 $AD$ 绕点 $D$ 逆时针旋转 $60^\circ$ 得到线段 $DE$，连接 $BE$．根据题意在图1中补全图形，并证明：$CD=BE$；
    标注
    • 题型
      >
      几何部分
      >
      几何模型
      >
      共顶点模型
    答案
    略
    解析
    解法一如图，连接 $AE$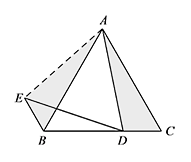．由旋转可得 $DA=DE$，$\angle ADE=60^\circ$，
    所以 $\triangle ADE$ 为等边三角形，
    从而 $AE=AD$，$\angle EAD=60^\circ=\angle BAC$，
    所以 $\angle EAB=\angle DAC$．
    而 $AB=AC$，
    所以 $\triangle AEB\cong \triangle ADC$，
    所以 $CD=BE$．
    解法二如图，过点 $D$ 作 $DF\parallel AB$ 交 $AC$ 于点 $F$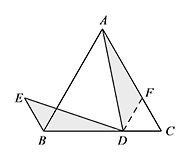．由已知可得 $\triangle CDF$ 为等边三角形，
    所以 $CD=CF=DF$，$\angle CDF=\angle CFD=60^\circ$，
    所以 $CA-CF=CB-CD$，即 $AF=DB$．
    由旋转可得 $AD=DE$，$\angle ADE=60^\circ$，
    所以 $\angle ADF+\angle EDB=60^\circ=\angle ADF+\angle DAF$，
    所以 $\angle EDB=\angle DAF$，
    从而 $\triangle DBE\cong AFD$，
    所以 $CD=DF=BE$．
    解法三如图，延长 $DB$ 至点 $G$，使得 $BG=CD$，连接 $EG$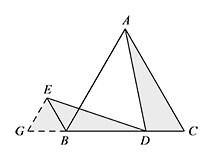．易证 $GD=BC=CA$．
    由旋转可得 $AD=DE$，$\angle ADE=60^\circ$，
    所以 $\angle EDG+\angle ADC=120^\circ=\angle DAC+\angle ADC$，
    从而 $\angle EDG=\angle DAC$，
    所以 $\triangle DEG\cong \triangle ADC$，
    所以 $\angle G=\angle C=60^\circ$，$GE=CD=GB$，
    所以 $\triangle BEG$ 为等边三角形，
    从而 $BE=BG=CD$．
  2. 如图2，若 $AB=AC=kBC$，$AD=kDE$，且 $\angle ADE=\angle C$，此时 $BE,BD,AC$ 三者之间的关系如何，并说明理由．
    标注
    • 题型
      >
      几何部分
      >
      几何模型
      >
      共顶点模型
    答案
    $AC=k(BE+BD)$
    解析
    解法一如图，连接 $AE$．由 $AC=kBC$，$AD=kDE$，$\angle ADE=\angle C$，
    可证 $\triangle ACB\backsim \triangle ADE$，
    所以 $\dfrac{AE}{AD}=\dfrac{AB}{AC}=1$，$\angle EAD=\angle BAC$，
    所以 $AE=AD$，$\angle EAB=\angle DAC$．
    而 $AB=AC$，
    所以 $\triangle AEB\cong \triangle ADC$，
    所以 $BE=CD$，
    从而 $AC=kBC=k(BE+BD)$．
    解法二如图，过点 $D$ 作 $DF\parallel AB$ 交 $AC$ 于点 $F$．则有 $\dfrac{AF}{BD}=\dfrac{CF}{CD}=\dfrac{AC}{BC}=k$，
    所以 $AF=kBD$，$DF=CF=kCD$．
    由 $\angle ADE=\angle C=\angle FDC$，
    可得 $\angle EDB+\angle ADF=\angle ADF+\angle DAF$，
    所以 $\angle EDB=\angle DAF$．
    而 $AD=kDE$，
    所以 $\triangle DBE\backsim \triangle AFD$，
    所以 $FD=kBE$，
    从而 $AC=AF+FC=k(BE+BD)$．
    解法三如图，延长 $DB$ 至点 $G$，使得 $BG=CD$，连接 $EG$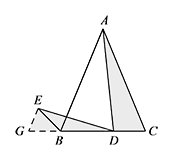．易证 $AC=kBC=kGD$．
    由 $\angle ADE=\angle C$，
    可得 $\angle EDG+\angle ADC=\angle ADC+\angle DAC$，
    所以 $\angle EDG=\angle DAC$．
    而 $AD=kDE$，
    所以 $\triangle DEG\backsim \triangle ADC$，
    所以 $\angle G=\angle C$，$BG=CD=kGE$，
    从而 $\triangle BEG\backsim \triangle ABC$，
    所以 $\dfrac{BE}{BG}=\dfrac{AB}{AC}=1$，
    所以 $AC=kGD=k(BE+BD)$．
题目 问题1 答案1 解析1 备注1 问题2 答案2 解析2 备注2
0.110300s