在数学兴趣小组活动中，小明进行数学探究活动．将边长为 $2$ 的正方形 $ABCD$ 与边长为 $2\sqrt 2$ 的正方形 $AEFG$ 按图 1 位置放置，$AD$ 与 $AE$ 在同一条直线上，$AB$ 与 $AG$ 在同一条直线上．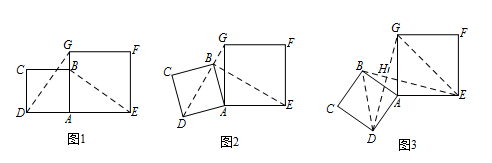
【难度】
【出处】
无
【标注】
-
小明发现 $DG\perp BE$，请你帮他说明理由．标注答案略解析因为四边形 $ABCD$ 与四边形 $AEFG$ 是正方形，
所以 $AD=AB$，$\angle DAG=\angle BAE=90^\circ$，$AG=AE$，
所以 $\triangle ADG\cong\triangle ABE$（$\mathrm {SAS}$），
所以 $\angle AGD=\angle AEB$．
如图，延长 $EB$ 交 $DG$ 于点 $H$．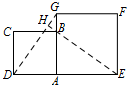
在 $\triangle ADG$ 中，$\angle AGD+\angle ADG=90^\circ $，
所以 $\angle AEB+\angle ADG=90^\circ$．
在 $\triangle DEH$ 中，$\angle AEB+\angle ADG+\angle DHE=180^\circ$，
所以 $\angle DHE=90^\circ$，
所以 $DG\perp BE$． -
如图 2，小明将正方形 $ABCD$ 绕点 $A$ 逆时针旋转，当点 $B$ 恰好落在线段 $DG$ 上时，请你帮他求出此时 $BE$ 的长．标注答案$BE$ 的长为 $\sqrt2+\sqrt6$解析因为四边形 $ABCD$ 与四边形 $AEFG$ 是正方形，
所以 $AD=AB$，$\angle DAB=\angle GAE=90^\circ$，$AG=AE$，
所以 $\angle DAB+\angle BAG=\angle GAE+\angle BAG$，
所以 $\angle DAG=\angle BAE$．
因为 $AD=AB$，$\angle DAG=\angle BAE$，$AG=AE$，
所以 $\triangle ADG\cong\triangle ABE$（$\mathrm {SAS}$），
所以 $DG=BE$．
如图，过点 $A$ 作 $AM\perp DG$ 交 $DG$ 于点 $M$，$\angle AMD=\angle AMG=90^\circ$．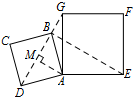
因为 $BD$ 是正方形 $ABCD$ 的对角线，
所以 $\angle MDA=45^\circ$．
在 $\mathrm {Rt}\triangle AMD$ 中，
因为 $\angle MDA=45^\circ$，
所以 $\cos{45^\circ}=\dfrac{DM}{AD}$，
所以 $DM=\sqrt 2$，
所以 $AM=\sqrt 2$．
在 $\mathrm {Rt}\triangle AMG$ 中，
因为 $AM^2+GM^2=AG^2$，
所以 $GM=\sqrt{AG^2-AM^2}=\sqrt{\left(2\sqrt2\right)^2-\left(\sqrt2\right)^2}$，
$GM=\sqrt6$，
因为 $DG=DM+GM=\sqrt2+\sqrt6$，
所以 $BE=DG=\sqrt2+\sqrt6$． -
如图 3，小明将正方形 $ABCD$ 绕点 $A$ 继续逆时针旋转，线段 $DG$ 与线段 $BE$ 将相交，交点为 $H$，写出 $\triangle GHE$ 与 $\triangle BHD$ 面积之和的最大值，并简要说明理由．标注答案$\triangle GHE$ 与 $\triangle BHD$ 面积之和的最大值为 $6$解析$\triangle GHE$ 与 $\triangle BHD$ 面积和的最大值为 $6$．
对于 $\triangle EGH$，点 $H$ 在以 $EG$ 为直径的圆上，
所以当点 $H$ 与点 $A$ 重合时，$\triangle EGH$ 的高最大，
对于 $\triangle BDH$，点 $H$ 在以 $BD$ 为直径的圆上，
所以当点 $H$ 与点 $A$ 重合时，$\triangle BDH$ 的高最大，
所以 $\triangle GHE$ 与 $\triangle BHD$ 面积之和的最大值为 $2+4=6$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
