如图,四边形 $ABCD,BEFG$ 均为正方形,连接 $AG,CE$.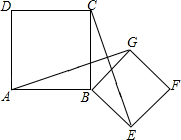

【难度】
【出处】
无
【标注】
-
求证:$AG=CE$;标注答案略解析因为四边形 $ABCD,BEFG$ 均为正方形,
所以 $AB=CB,\angle ABC=\angle GBE=90^\circ,BG=BE,$
所以 $\angle ABG=\angle CBE$,
所以 $\triangle ABG\cong \triangle CBE$,
所以 $AG=CE$. -
求证:$AG\perp CE$.标注答案略解析因为 $\triangle ABG\cong \triangle CBE$,
所以 $\angle BAG=\angle BCE$,
因为 $\angle ABC=90^\circ$,
所以 $\angle BAG+\angle AMB=90^\circ$,
因为 $\angle AMB=\angle CMN$,
所以 $\angle BCE+\angle CMN=90^\circ$,
所以 $\angle CNM=90^\circ$,
所以 $AG\perp CE$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2