如图，在 $\triangle ABC$ 中，$\angle ACB=90^\circ$，$AB=AC$，点 $E$ 是 $AC$ 上一点，连接 $BE$，点 $D$ 是线段 $BE$ 延长线上一点，过点 $A$ 作 $AF\perp BD$ 于点 $F$，连接 $CD,CF$，当 $AF=DF$ 时，求证：$DC=BC$．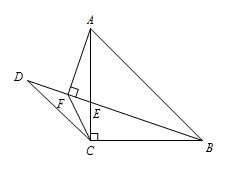
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
如图，过点 $C$ 作 $CM\perp CF$ 交 $BD$ 于点 $M$，
所以 $\angle FCM=90^\circ$，
因为 $\angle ACB=90^\circ$，所以 $\angle FCA=\angle MCB$，
因为 $AF\perp BD$，所以 $\angle AFB=90^\circ$，
所以 $\angle AFE=\angle ACB$，
因为 $\angle AEF=\angle BEC$，
所以 $\angle CAF=\angle CBM$，
所以 $\triangle ACF\cong \triangle BCM$，
所以 $FC=MC$，
又因为 $\angle FCM=90^\circ$，
所以 $\angle CFM=\angle CMF=45^\circ$，
所以 $\angle AFC=\angle AFB+\angle CFM=135^\circ$，$\angle DFC=180^\circ-\angle CFM=135^\circ$，
所以 $\angle AFC=\angle DFC$，
所以 $\triangle ACF\cong \triangle DCF$，
所以 $AC=DC$，
因为 $AC=BC$，所以 $DC=BC$．
所以 $\angle FCM=90^\circ$，因为 $\angle ACB=90^\circ$，所以 $\angle FCA=\angle MCB$，
因为 $AF\perp BD$，所以 $\angle AFB=90^\circ$，
所以 $\angle AFE=\angle ACB$，
因为 $\angle AEF=\angle BEC$，
所以 $\angle CAF=\angle CBM$，
所以 $\triangle ACF\cong \triangle BCM$，
所以 $FC=MC$，
又因为 $\angle FCM=90^\circ$，
所以 $\angle CFM=\angle CMF=45^\circ$，
所以 $\angle AFC=\angle AFB+\angle CFM=135^\circ$，$\angle DFC=180^\circ-\angle CFM=135^\circ$，
所以 $\angle AFC=\angle DFC$，
所以 $\triangle ACF\cong \triangle DCF$，
所以 $AC=DC$，
因为 $AC=BC$，所以 $DC=BC$．
答案
解析
备注
