如图1，在四边形 $ABCD$ 中，点 $E,F$ 分别是 $AB$，$CD$ 的中点，过点 $E$ 作 $AB$ 的垂线，过点 $F$ 作 $CD$ 的垂线，两垂线交于点 $G$，连接 $AG,BG,CG,DG$，且 $\angle AGD=\angle BGC$．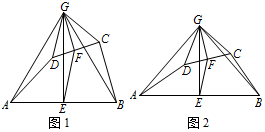
【难度】
【出处】
无
【标注】
-
求证：$AD=BC$；标注答案略解析因为 $GE$ 是 $AB$ 的垂直平分线，
所以 $GA=GB$，
同理可得 $GD=GC$．
在 $\triangle AGD$ 和 $\triangle BGC$ 中，
$\begin{cases}GA=GB, \\ \angle AGD=\angle BGC, \\ GD=GC, \end{cases}$
所以 $\triangle AGD\cong \triangle BGC$（${\mathrm {SAS}}$），
所以 $AD=BC$． -
求证：$\triangle AGD\backsim \triangle EGF$；标注答案略解析因为 $\angle AGD=\angle BGC$，
所以 $\angle AGB=\angle DGC$，
在 $\triangle AGB$ 和 $\triangle DGC$ 中，$\dfrac {GA}{GD}=\dfrac {GB}{GC}$，
所以 $\triangle AGB\backsim \triangle DGC$，
所以 $\dfrac {EG}{FG}=\dfrac {GA}{GD}$．
又 $\angle AGE=\angle DGF$，
所以 $\angle AGD=\angle EGF$，
所以 $\triangle AGD \backsim \triangle EGF$． -
如图 2，若 $AD,BC$ 所在直线互相垂直，求 $\dfrac {AD}{EF}$ 的值．标注答案$\dfrac {AD}{EF}$ 的值为 $\sqrt 2$解析延长 $AD$ 交 $GB$ 于点 $M$，交 $BC$ 的延长线于点 $H$，如图所示．
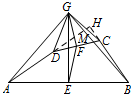则 $AH\perp BH$，．
因为 $\triangle AGD\cong \triangle BGC$，
所以 $\angle GAD=\angle GBC$，
在 $\triangle GAM$ 和 $\triangle HBM$ 中，$\angle GAD=\angle GBC$，$\angle GMA=\angle HMB$，
所以 $\angle AGB=\angle AHB=90^\circ $，
所以 $\angle AGE=\dfrac12 \angle AGB=45^\circ $，
所以 $\dfrac {AG}{EG}=\sqrt 2$，
又 $\triangle AGD\backsim \triangle EGF$，
所以 $\dfrac {AD}{EF}=\dfrac {AG}{EG}=\sqrt 2$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
