点 $P$ 是四边形 $ABCD$ 内一点，且满足 $PA=PB$，$PC=PD$，$\angle APB=\angle CPD$，
【难度】
【出处】
无
【标注】
-
点 $E,F,G,H$ 分别为边 $AB,BC,CD,DA$ 的中点，猜想中点四边形 $EFGH$ 的形状，并证明你的猜想．标注答案四边形 $EFGH$ 是菱形解析连接 $AC,BD$．
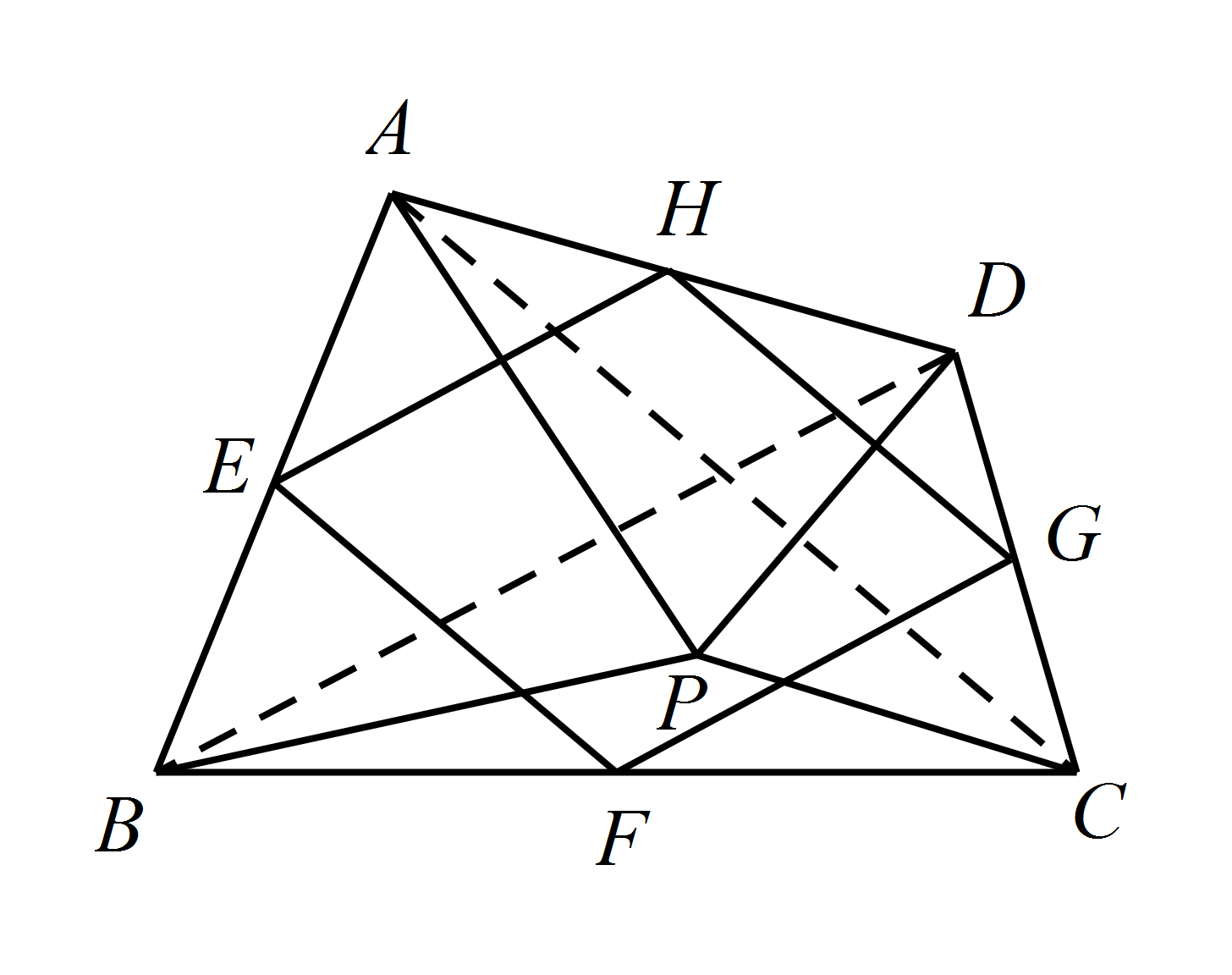因为 $\angle APB=\angle CPD$，
所以 $\angle APB+\angle APD=\angle CPD+\angle APD$，即 $\angle APC=\angle BPD$．
在 $\triangle APC$ 和 $\triangle BPD$ 中，
$\begin{cases} AP=PB,\\ \angle APC= \angle BPD,\\PC=PD,\end{cases}$
所以 $\triangle APC\cong\triangle BPD$，
所以 $AC=BD$．
因为点 $E,F,G$ 分别为边 $AB,BC,CD$ 的中点，
所以 $EF=\dfrac{1}{2} AC$，$FG=\dfrac{1}{2} BD$，
因为四边形 $EFGH$ 是平行四边形，
所以四边形 $EFGH$ 是菱形． -
若使 $\angle APB=\angle CPD=90^\circ$，其他条件不变，直接写出中点四边形 $EFGH$ 的形状．标注答案四边形 $EFGH$ 是正方形解析设 $AC$ 与 $BD$ 交于点 $O$．$AC$ 与 $PD$ 交于点 $M$，$AC$ 与 $EH$ 交于点 $N$．
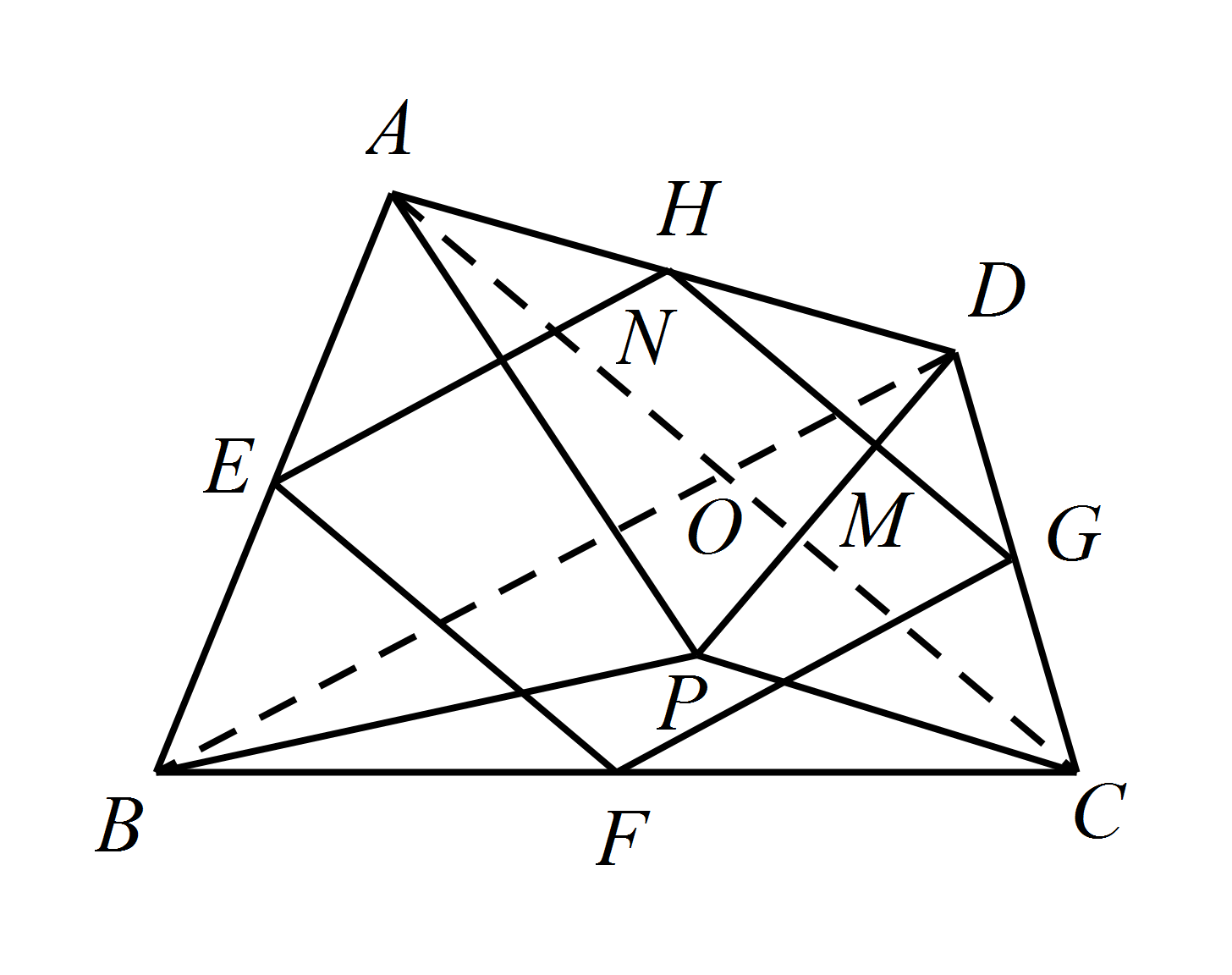因为 $\triangle APC\cong\triangle BPD$，
所以 $\angle ACP=\angle BDP$，
因为 $\angle DMO=\angle CMP$，
所以 $\angle COD=\angle CPD=90^\circ $，
因为 $EH\parallel BD$，$AC\parallel HG$，
所以 $\angle EHG=\angle ENO=\angle BOC=\angle DOC=90^\circ$，
因为四边形 $EFGH$ 是菱形，
所以四边形 $EFGH$ 是正方形．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
