【图形定义】
如图，将正 $n$ 边形绕点 $A$ 顺时针旋转 $60^\circ$ 后，发现旋转前后两图形有另一交点 $O$，连接 $AO$，我们称 $AO$ 为“叠弦”；再将“叠弦”$AO$ 所在的直线绕点 $A$ 逆时针旋转 $60^\circ$ 后，交旋转前的图形于点 $P$，连接 $PO$，我们称 $\angle OAB$ 为“叠弦角”，$\triangle AOP$ 为“叠弦三角形”．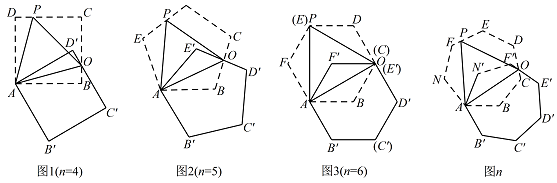
如图，将正 $n$ 边形绕点 $A$ 顺时针旋转 $60^\circ$ 后，发现旋转前后两图形有另一交点 $O$，连接 $AO$，我们称 $AO$ 为“叠弦”；再将“叠弦”$AO$ 所在的直线绕点 $A$ 逆时针旋转 $60^\circ$ 后，交旋转前的图形于点 $P$，连接 $PO$，我们称 $\angle OAB$ 为“叠弦角”，$\triangle AOP$ 为“叠弦三角形”．
【难度】
【出处】
无
【标注】
-
【探究证明】
（i）请在图1和图2中选择其中一个证明：“叠弦三角形”（即 $\triangle AOP$）是等边三角形；
（ii）如图2，求证：$\angle OAB=\angle OAE'$．标注答案略解析（i）因为四边形 $ABCD$ 是正方形，
由旋转知 $AD=AD'$，$\angle D=\angle D'=90^\circ$，$\angle DAD'=\angle OAP=60^\circ$．
所以 $\angle DAP=\angle D'AO$．
所以 $\triangle APD\cong \triangle AOD'$ $\mathrm {\left(ASA\right)}$．
所以 $AP=AO$，又 $\angle OAP=60^\circ$，
所以 $\triangle AOP$ 是等边三角形．
（ii）如下图，作 $AM\perp DE$ 于 $M$，作 $AN\perp CB$ 于 $N$．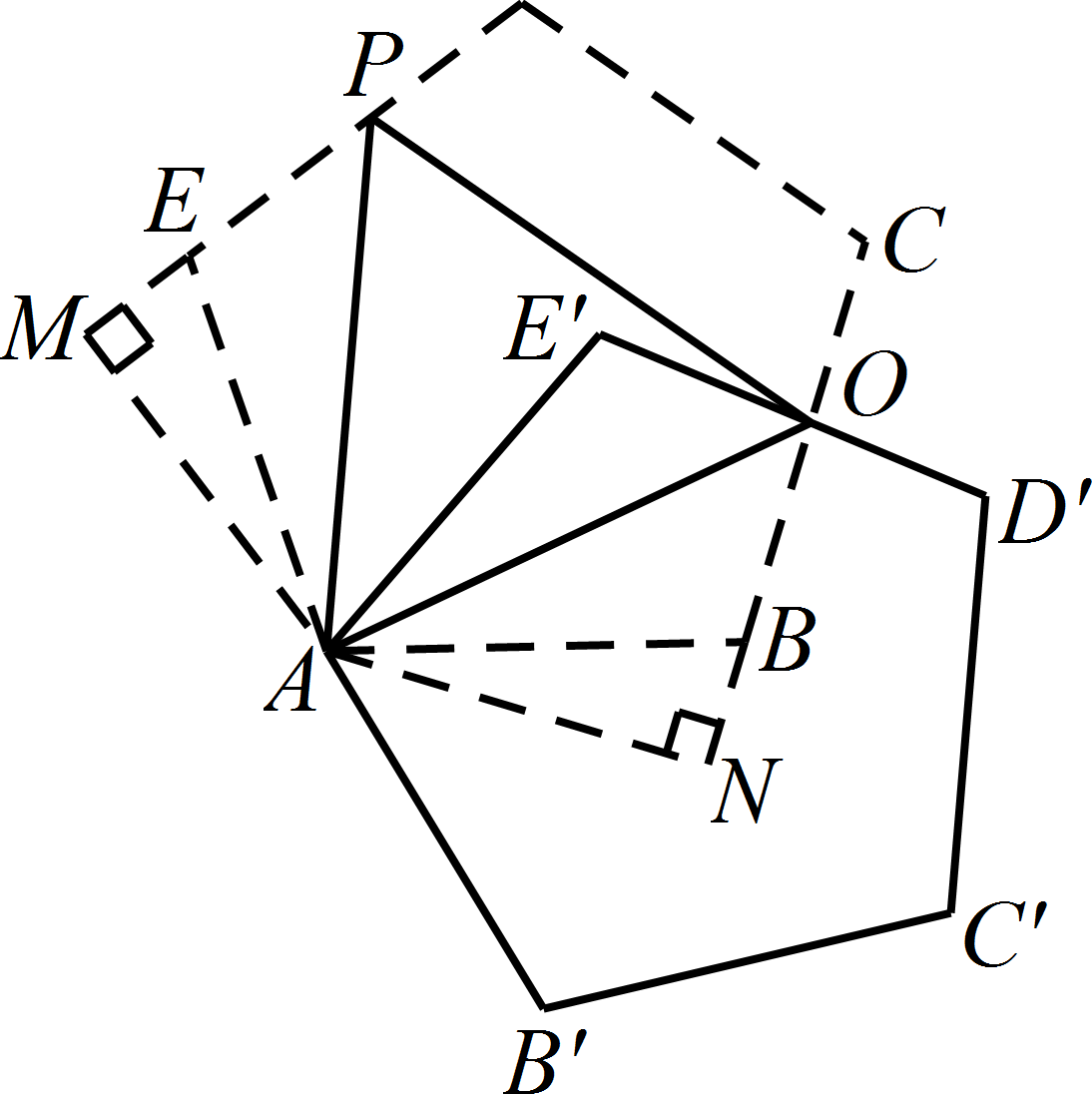
因为五边形 $ABCDE$ 是正五边形，
由旋转知：$AE=AE'$，$\angle E=\angle E'=108^\circ$，$\angle EAE'=\angle OAP=60^\circ$．
所以 $\angle EAP=\angle E'AO$．
所以 $\triangle APE\cong \triangle AOE'$ $\mathrm {\left(ASA\right)}$．
所以 $\angle OAE'=\angle PAE$．
在 $\mathrm {Rt}\triangle AEM$ 和 $\mathrm {Rt}\triangle ABN$ 中，
$\begin{cases}\angle M=\angle N=90^\circ,\\
\angle AEM=\angle ABN=72^\circ,\\
AE=AB\end{cases}$
所以 $\mathrm {Rt}\triangle AEM\cong \mathrm {Rt}\triangle ABN$ $\mathrm {\left(AAS\right)}$
所以 $\angle EAM=\angle BAN$，$AM=AN$．
在 $\mathrm {Rt}\triangle APM$ 和 $\mathrm {Rt}\triangle AON$ 中，
$\begin{cases}AP=AO,\\
AM=AN.\end{cases}$
所以 $\mathrm {Rt}\triangle APM\cong \mathrm {Rt}\triangle AON$ $\mathrm {\left(HL\right)}$．
所以 $\angle PAM=\angle OAN$，
所以 $\angle PAE=\angle OAB$，
所以 $\angle OAE'=\angle OAB$． -
【归纳猜想】
（i）图1、图2中“叠弦角”的度数分别为
（ii）图n中，“叠弦三角形”
（ii）图n中，“叠弦角”的度数为
（ii）是
（iii）$60^\circ-\dfrac{180^\circ}{n}$解析（iii）$\angle OAB=\left[\left(n-2\right) \times 180^\circ\div n-60^\circ\right] \div 2 =60^\circ-\dfrac{180^\circ}{n}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
