如图 ①，$\triangle ABC$ 中，$\angle ABC=45^\circ$，$AH\perp BC$ 于点 $H$，点 $D$ 在 $AH$ 上，且 $DH=CH$，连接 $BD$．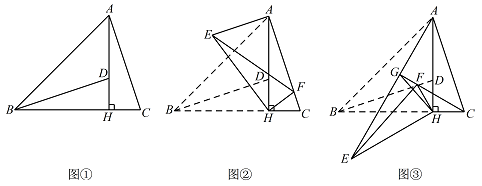
【难度】
【出处】
无
【标注】
-
求证：$BD=AC$；标注答案略解析在 $\mathrm {Rt}\triangle AHB$ 中，$\angle ABC=45^\circ$，
所以 $AH=BH$．
又因为 $\angle BHD=\angle AHC=90^\circ$，$DH=CH$，
所以 $\triangle BHD\cong \triangle AHC$ $\mathrm {\left(SAS\right)}$，
所以 $BD=AC$． -
将 $\triangle BHD$ 绕点 $H$ 旋转，得到 $\triangle EHF$（点 $B$，$D$ 分别与点 $E$，$F$ 对应），连接 $AE$．
（i）如图 ②，当点 $F$ 落在 $AC$ 上时（$F$ 不与 $C$ 重合），若 $BC=4$，$\tan \angle C=3$，求 $AE$ 的长；
（ii）如图 ③，当 $\triangle EHF$ 是由 $\triangle BHD$ 绕点 $H$ 逆时针旋转 $30^\circ$ 得到时，设射线 $CF$ 与 $AE$ 相交于点 $G$，连接 $GH$，试探究线段 $GH$ 与 $EF$ 之间满足的等量关系，并说明理由．标注答案（i）$AE=\dfrac{3\sqrt{10}}{5}$；
（ii）$\dfrac{EF}{HG}=\dfrac{1}{2}$解析（i）在 $\mathrm {Rt}\triangle AHC$ 中，$\tan \angle C=3$，
所以 $\dfrac{AH}{HC}=3$．
设 $CH=x$，则 $BH=AH=3x$，
因为 $BC=4$，
所以 $3x+x=4$，
所以 $x=1$．$AH=3$，$CH=1$．
由旋转知 $\angle EHF=\angle BHD=\angle AHC=90^\circ$，$EH=AH=3$，$CH=DH=FH$．
所以 $\angle EHA=\angle FHC$，$\dfrac{EH}{AH}=\dfrac{FH}{HC}=1$，
所以 $\triangle EHA\backsim \triangle FHC$，
所以 $\angle EAH=\angle C$，
所以 $\tan \angle EAH=\tan \angle C=3$．
如图 ④，过点 $H$ 作 $HP\perp AE$ 于 $P$，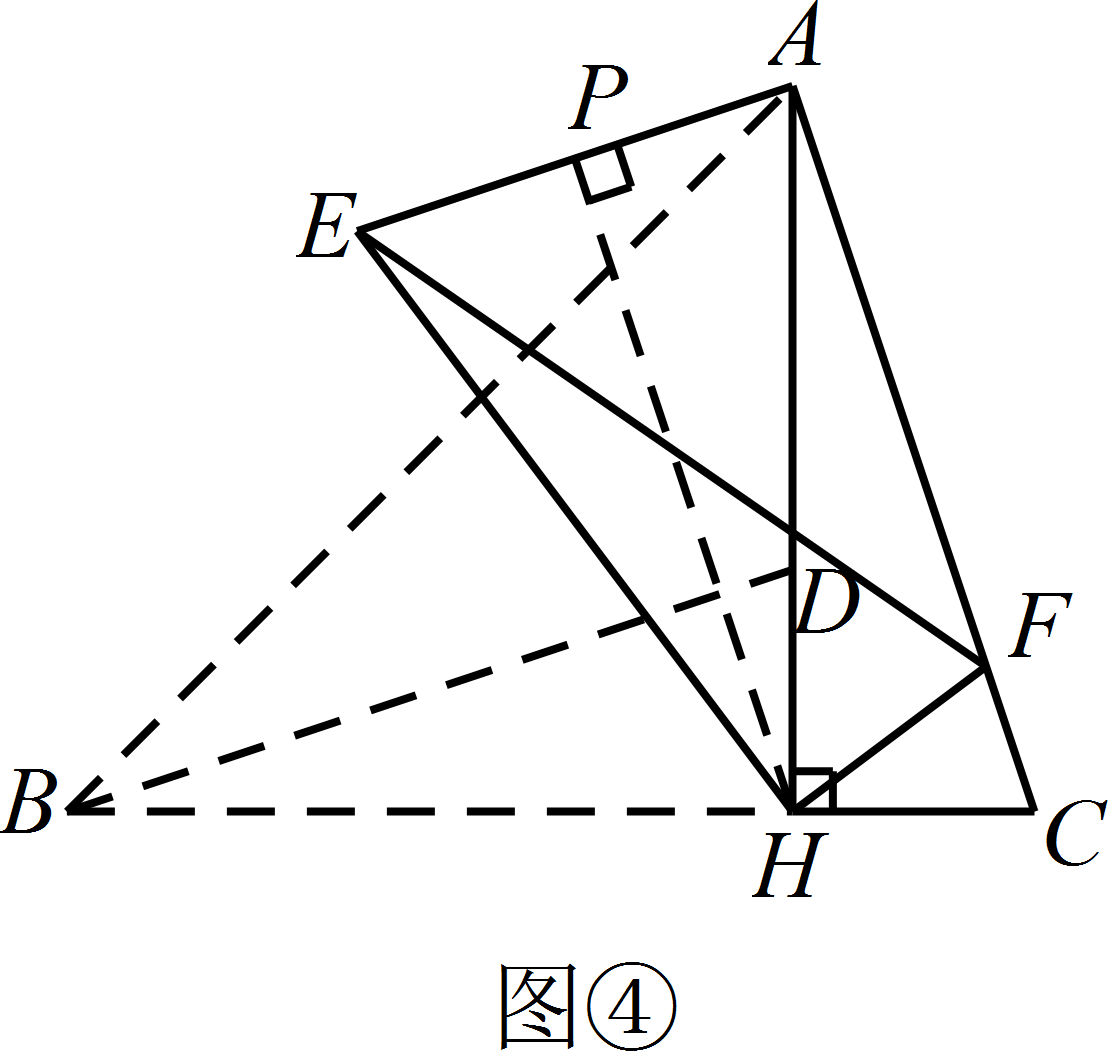
则 $HP=3AP$，$AE=2AP$．
在 $\mathrm {Rt}\triangle AHP$ 中，$AP^{2}+HP^{2}= AH^{2}$，
所以 $AP^{2}+\left(3AP\right)^{2}= 9$，解得 $AP=\dfrac{3\sqrt{10}}{10}$，$AE=\dfrac{3\sqrt{10}}{5}$．
（ii）由题意及已证可知，$\triangle AEH和\triangle FHC$ 均为等腰三角形，
所以 $\angle GAH=\angle HCG=30^\circ$，
所以 $\triangle AGQ\backsim \triangle CHQ$，
所以 $\dfrac{AQ}{CQ}=\dfrac{GQ}{HQ}$，
所以 $\dfrac{AQ}{GQ}=\dfrac{CQ}{HQ}$．
又因为 $\angle AQC=\angle GQE$，
所以 $\triangle AQC\backsim \triangle GQH$，
所以 $\dfrac{EF}{HG}=\dfrac{AC}{GH}=\dfrac{AQ}{GQ}=\sin 30^\circ=\dfrac{1}{2}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
