如图1，$\triangle ABC$ 是等腰直角三角形，$\angle BAC=90^\circ$，$AB=AC$，四边形 $ADEF$ 是正方形，点 $B$，$C$ 分别在边 $AD$，$AF$ 上，此时 $BD=CF$，$BD\perp CF$ 成立．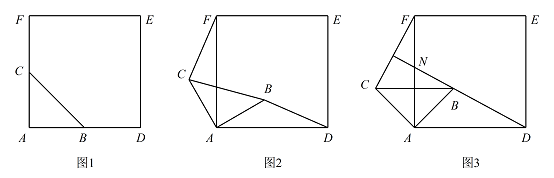
【难度】
【出处】
无
【标注】
-
当 $\triangle ABC$ 绕点 $A$ 逆时针旋转 $\theta \left(0^\circ <\theta <90^\circ \right)$ 时，如图2，$BD=CF$ 成立吗？若成立，请证明；若不成立，请说明理由．标注答案$BD=CF$ 成立解析因为 $AC=AB$，$\angle CAF=\angle BAD=\theta$，$AF=AD$，
所以 $\triangle ABD \cong \triangle ACF$，
所以 $BD=CF$． -
当 $\triangle ABC$ 绕点 $A$ 逆时针旋转 $45^\circ $ 时，如图3，延长 $DB$ 交 $CF$ 于点 $H$．
（i）求证：$BD\perp CF$；
（ii）当 $AB=2$，$AD=3\sqrt{2}$ 时，求线段 $DH$ 的长．标注答案（ii）$DH=\dfrac {9\sqrt{10}} 5$解析（i）由第1问可得 $\triangle ABD \cong \triangle ACF$，
所以 $\angle HFN=\angle ADN$，
在 $\triangle HFN$ 与 $\triangle ADN$ 中，
因为 $\angle HFN=\angle ADN$，$\angle HNF=\angle AND$，
所以 $\angle NHF=\angle NAD=90^\circ$，
所以 $HD\perp HF$，即 $BD\perp CF$．
（ii）如图，连接 $DF$，延长 $AB$ 到点 $M$，与 $DF$ 交于点 $M$．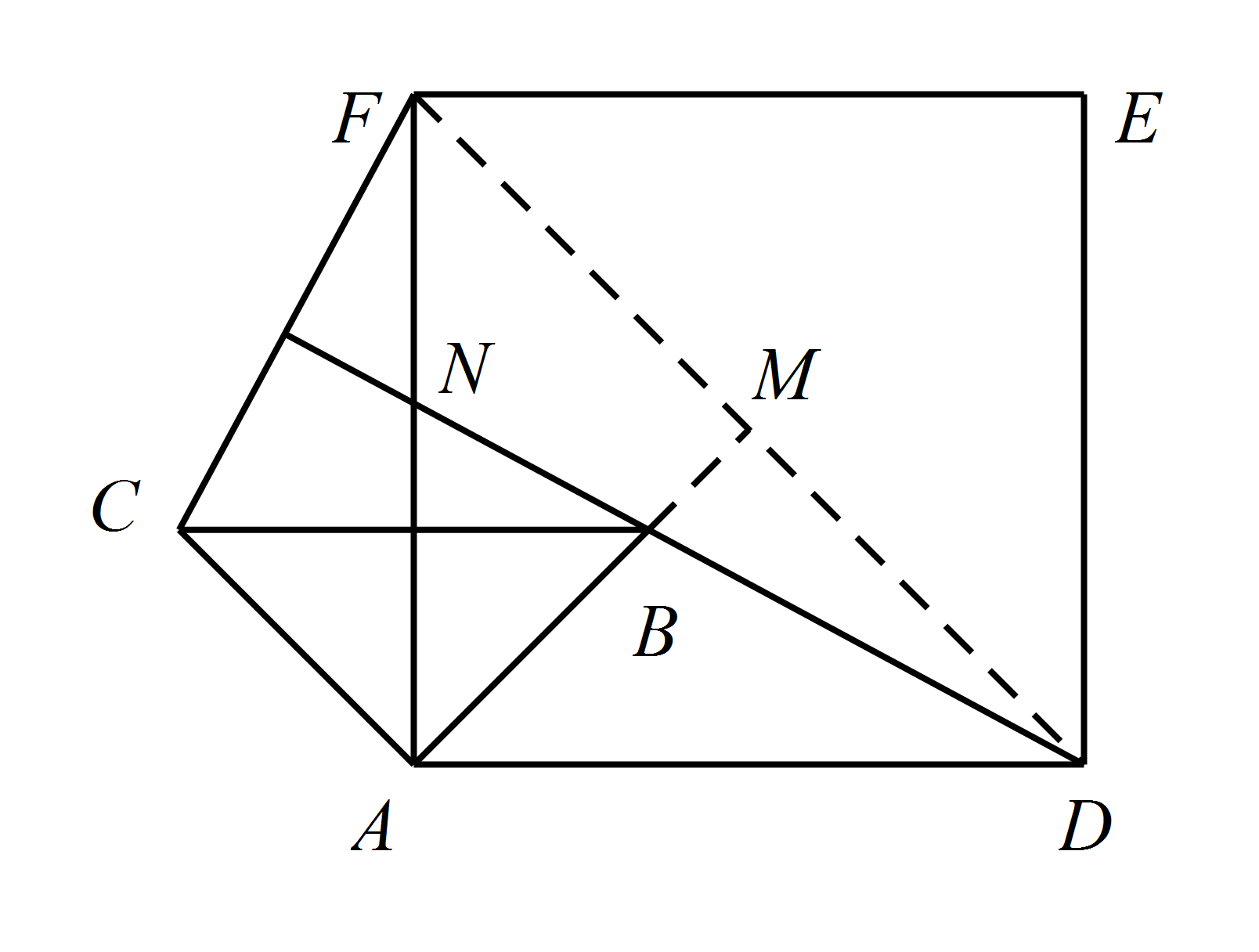
在 $\triangle MAD$ 中，
因为 $\angle MAD=\angle MDA=45^\circ$，
所以 $\angle BMD=90^\circ$．
在 $\mathrm {Rt}\triangle BMD$ 与 $\mathrm{Rt}\triangle FHD$ 中，
因为 $\angle MDB=\angle HDF$，
所以 $\triangle BMD \backsim \triangle FHD$．
因为 $AB=2$，$AD=3\sqrt{2}$，四边形 $ADEF$ 是正方形，
所以 $MA=MD=\dfrac {3\sqrt{2}} {\sqrt{2}} =3$，
所以 $MD=3-2=1$，$DB=\sqrt{1^2+3^2}=\sqrt{10}$，
$\dfrac {MD} {HD} =\dfrac {BD} {FD}$，即 $\dfrac 3{HD} =\dfrac {\sqrt{10}} 6$，
所以 $DH=\dfrac {9\sqrt{10}} 5$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
