如图，四边形 $ABCD$ 中，$AB=AD$，$AB\perp AD$，连接 $AC$，过点 $A$ 作 $AE\perp AC$，且使 $AE=AC$，连接 $BE$，过点 $A$ 作 $AH\perp CD$ 于点 $H$，交 $BE$ 于点 $F$．请你判断 $BF,EF$ 的数量关系，并说明理由．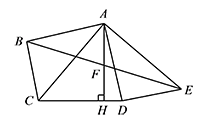
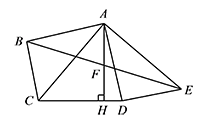
【难度】
【出处】
无
【标注】
【答案】
$BE=EF$
【解析】
如图，将 $\triangle ACD$ 绕点 $A$ 逆时针旋转 $90^\circ$，得到 $\triangle AEG$．
显然点 $B,A,G$ 三点共线．
由旋转的性质可得 $GE\perp CD$，
所以 $GE\parallel AH$，
从而 $\dfrac{BA}{AG}=\dfrac{BF}{FE}$．
而 $AB=AD=AG$，
所以 $BF=FE$．
显然点 $B,A,G$ 三点共线．由旋转的性质可得 $GE\perp CD$，
所以 $GE\parallel AH$，
从而 $\dfrac{BA}{AG}=\dfrac{BF}{FE}$．
而 $AB=AD=AG$，
所以 $BF=FE$．
答案
解析
备注
