如图，若 $\triangle ABC$ 与 $\triangle DEF$ 都是等腰三角形，$AB,EF$ 的中点均为 $O$，且顶角 $\angle ACB=\angle EDF=\alpha$，直线 $BF,CD$ 交于点 $G$，连接 $AG$．现将图中 $\triangle DEF$ 绕点 $O$ 旋转，请你确定 $AG$ 取最小值和最大值时点 $G$ 的位置．
【难度】
【出处】
无
【标注】
【答案】
以 $BC$ 为直径的 $\odot H$，直线 $AH$ 交 $\odot H$ 于点 $G_1,G_2$，则 $G_1$ 为 $AG$ 取最小值时点 $G$ 的位置，$G_2$ 为 $AG$ 取最大值时点 $G$ 的位置
【解析】
如图，连接 $CO,DO$．
则 $\triangle COB\sim \triangle DOF$，
从而得 $\triangle BOF\sim \triangle COD$，
所以 $\angle OBF=\angle OCD$．
易证 $\angle BGC=\angle BOC=90^\circ$．
故点 $G$ 在以 $BC$ 为直径的圆上．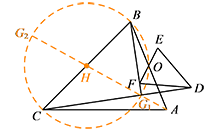
如图，以 $BC$ 为直径的 $\odot H$，直线 $AH$ 交 $\odot H$ 于点 $G_1,G_2$，则 $G_1$ 为 $AG$ 取最小值时点 $G$ 的位置，$G_2$ 为 $AG$ 取最大值时点 $G$ 的位置．
则 $\triangle COB\sim \triangle DOF$，从而得 $\triangle BOF\sim \triangle COD$，
所以 $\angle OBF=\angle OCD$．
易证 $\angle BGC=\angle BOC=90^\circ$．
故点 $G$ 在以 $BC$ 为直径的圆上．
如图，以 $BC$ 为直径的 $\odot H$，直线 $AH$ 交 $\odot H$ 于点 $G_1,G_2$，则 $G_1$ 为 $AG$ 取最小值时点 $G$ 的位置，$G_2$ 为 $AG$ 取最大值时点 $G$ 的位置．
答案
解析
备注
