在平行四边形 $ABCD$ 中，$\angle A=\angle DBC$，过点 $D$ 作 $DE=DF$，且 $\angle EDF=\angle ABD$，连接 $EF,EC$，$N,P$ 分别为 $EC,BC$ 的中点，连接 $NP$．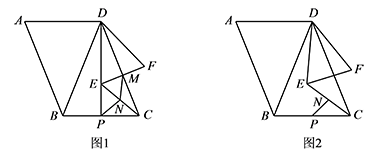
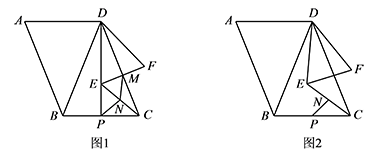
【难度】
【出处】
无
【标注】
-
如图1，若点 $E$ 在 $DP$ 上，$EF$ 与 $DC$ 交于点 $M$，试探究线段 $NP$ 与线段 $NM$ 的数量关系及 $\angle ABD$ 与 $\angle MNP$ 满足的等量关系；标注答案$NP=MN$，$\angle ABD+\angle MNP=180^\circ$解析
解法一 因为 $\angle DCB=\angle A=\angle DBC$，
所以 $ \triangle DBC $ 是等腰三角形，
而点 $P$ 为 $BC$ 中点，
所以 $DP\perp BC$，$\angle PDC=\dfrac 12 \angle BDC=\dfrac 12\angle ABD=\dfrac 12\angle EDF$．
又 $DE=DF$，
所以 $EM=FM$，$CD\perp EF$，
所以 $NP=\dfrac 12 CE=NM$．
所以 $\angle MNP=2\angle NCP+2\angle NCM=2\angle DCB$，
即 $\angle ABD+\angle MNP=\angle BDC+2\angle DCB=180^\circ$．解法二 如图，连接 $BE,CF$．
由 $\angle DCB=\angle A=\angle DBC$，可得 $DB=DC$．
而点 $P$ 为 $BC$ 中点，
所以 $\angle PDC=\dfrac 12 \angle BDC=\dfrac 12\angle ABD=\dfrac 12\angle EDF$．
又 $DE=DF$，
所以 $EM=FM$．
从而 $NP\parallel BE$，$NP=\dfrac 12EB$，$NM\parallel CF$，$NM=\dfrac 12CF$．
易证 $\triangle DBE\cong \triangle DCF$，
所以 $BE=CF$，$\angle DBE=\angle DCF$，
所以 $NP=NM$，且
$\begin{split}\angle ABD+\angle MNP&=\angle BDC+\angle MNE+\angle PNE\\ &=\angle BDC+\angle FCE+\angle ECB+\angle NPC\\ &=\angle BDC+\angle FCD+\angle DCB+\angle EBC\\ &=\angle BDC+\angle DBC+\angle DCB=180^\circ.\end{split}$ -
如图2，若点 $M$ 在线段 $EF$ 上，当点 $M$ 在何位置时，你在第1问中得到的结论仍然成立，写出你确定的点 $M$ 的位置，并证明第1问中的结论．标注答案点 $M$ 是线段 $EF$ 的中点解析如图所示，连接 $BE,CF$．
由等腰三角形共顶点模型可得 $BE=CF$，$\angle DBE=\angle DCF$．
取 $EF$ 的中点 $G$，连接 $NG$，
则 $PN\parallel BE$，$PN=\dfrac 12 BE$，$NG\parallel CF$，$NG=\dfrac 12 CF$．
所以 $PN=NG$，且
$\begin{split}\angle ABD+\angle GNP&=\angle BDC+\angle GNE+\angle PNE\\ &=\angle BDC+\angle FCE+\angle ECB+\angle NPC\\ &=\angle BDC+\angle FCD+\angle DCB+\angle EBC\\ &=\angle BDC+\angle DBC+\angle DCB=180^\circ.\end{split}$
所以当点 $M$ 与点 $G$ 重合，即为线段 $EF$ 的中点时，第1问中得到的结论仍然成立．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
