如图所示,在 $\triangle{ABC}$ 中,$AB=AC$,有一个圆内切于 $\triangle{ABC}$ 的外接圆,且与 $AB,AC$ 分别相切于 $P,Q$,求证:线段 $PQ$ 的中点 $O$ 是 $\triangle{ABC}$ 的内心.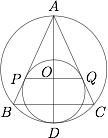

【难度】
【出处】
2009年全国高中数学联赛吉林省预赛
【标注】
【答案】
略
【解析】
设小圆圆心为 $O_1$,$\odot O_1$ 与 $\triangle{ABC}$ 的外接圆切于 $D$.
连结 $AO_1$,显然 $AO_1\perp PQ$,且 $\triangle{ABC}$ 为等腰三角形,所以 $AO_1$ 过 $\triangle{ABC}$ 的外接圆,$D$ 在 $AO_1$ 的延长线上,从而 $O$ 为 $\triangle{ABC}$ 的顶角 $\angle{BAC}$ 的平分线上的点,下面只需要证 $OB$ 平分 $\angle{ABC}$.
为此,连结 $OB,PD,QD$,由对称性易知,$OD$ 平分 $\angle{PDQ}$,而 $\angle{APQ}=\angle{PDQ}$,$PQ\parallel BC$,故$$\angle{APQ=\angle{ABC}},\angle{PDQ}=\angle{ABC},$$由 $P,B,D,Q$ 四点共圆得$$\angle{PBO}=\angle{PDO}=\dfrac 12 \angle{PDQ},$$所以 $\angle{PBO}=\dfrac 12 \angle{ABC}$,于是 $O$ 为 $\triangle{ABC}$ 的内心.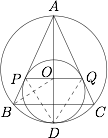
连结 $AO_1$,显然 $AO_1\perp PQ$,且 $\triangle{ABC}$ 为等腰三角形,所以 $AO_1$ 过 $\triangle{ABC}$ 的外接圆,$D$ 在 $AO_1$ 的延长线上,从而 $O$ 为 $\triangle{ABC}$ 的顶角 $\angle{BAC}$ 的平分线上的点,下面只需要证 $OB$ 平分 $\angle{ABC}$.
为此,连结 $OB,PD,QD$,由对称性易知,$OD$ 平分 $\angle{PDQ}$,而 $\angle{APQ}=\angle{PDQ}$,$PQ\parallel BC$,故$$\angle{APQ=\angle{ABC}},\angle{PDQ}=\angle{ABC},$$由 $P,B,D,Q$ 四点共圆得$$\angle{PBO}=\angle{PDO}=\dfrac 12 \angle{PDQ},$$所以 $\angle{PBO}=\dfrac 12 \angle{ABC}$,于是 $O$ 为 $\triangle{ABC}$ 的内心.

答案
解析
备注