查看数据源：5938c288ad99bb0008d76a81
在正方形 $ABCD$ 和正方形 $DEFG$ 中，顶点 $B,D,F$ 在同一直线上，$H$ 是 $BF$ 的中点，连接 $AH,GH$，证明：$AH=AG,AH\perp GH$．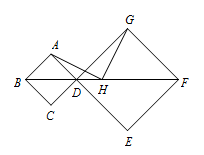
【难度】
【出处】
无
【标注】
  • 题型
    >
    几何部分
    >
    几何模型
    >
    共顶点模型
  • 题型
    >
    几何部分
    >
    几何模型
    >
    弦图模型
【答案】
略
【解析】
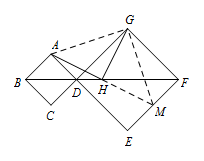解法一延长 $AH$ 交 $EF$ 于点 $M$，连接 $AG,GM$．因为正方形中 $ABCD$ 和正方形 $DEFG$ 且 $B,D,F$ 共线，
所以 $AB\parallel EF$，
所以 $\angle ABH=\angle MFH$，
又因为 $BH=FH,\angle AHB=\angle MHF$，
所以 $\triangle ABH\cong \triangle MFH$，
所以 $AH=MH,AB=MF$，
因为 $AB=AD$，
所以 $AD=MF$，
因为 $DG=FG,\angle ADG=\angle MFG=90^\circ$，
所以 $\triangle ADG\cong \triangle MFG$，
所以 $\angle AGD=\angle MGF,AG=MG$，
又因为 $\angle DGM+\angle MGF=90^\circ$，
所以 $\angle AGD+\angle DGM=90^\circ$，
所以 $\triangle AGM$ 为等腰直角三角形，
因为 $AH=MH$，
所以 $AH=GH,AH\perp GH$．
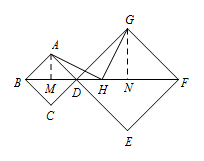解法二过点 $A,G$ 作 $AM\perp BF,GN\perp BF$ 交 $BF$ 于点 $M,N$．因为正方形中 $ABCD$ 和正方形 $DEFG$ 且 $B,D,F$ 共线，
所以 $AC\perp BF,GE\perp BF,DM=\dfrac 12BD,DN=\dfrac 12DF$，
所以 $\angle AMD=\angle GNH=90^\circ,MN=\dfrac 12 BF$，
因为 $H$ 是 $BF$ 的中点，
所以 $BH=\dfrac 12BF$，
所以 $BH=MN$，
所以 $BH-MH=MN-MH$，
所以 $BM=NH$，
因为 $AM=BM=DM$，
所以 $AM=HN=DM$，
所以 $MD+DH=NH+DH$，
所以 $MH=DN$，
因为 $DN=GN$，
所以 $MH=GN$，
所以 $\triangle AMH\cong \triangle HNG$，
所以 $AH=GH,\angle AHM=\angle HGN$，
因为 $\angle HGN+\angle GHN=90^\circ$，
所以 $\angle AHM+\angle GHN=90^\circ$，
所以 $\angle AHG=90^\circ$，
所以 $AH\perp GH$．
答案 解析 备注
0.130713s