已知正方形 $ABCD$ 的边长为 $4$,一个以点 $A$ 为顶点的 $45^\circ $ 角绕点 $A$ 旋转,角的两边分别与边 $BC$,$DC$ 的延长线交于点 $E$,$F$,连接 $EF$.设 $CE=a$,$CF=b$.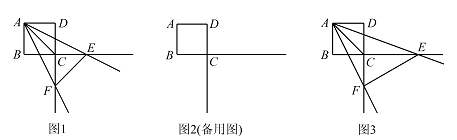

【难度】
【出处】
无
【标注】
-
如图1,当 $\angle EAF$ 被对角线 $AC$ 平分时,求 $a,b$ 的值;标注答案$a=b=4\sqrt 2$解析因为四边形 $ABCD$ 是正方形,
所以 $\angle BCF=\angle DCE=90^\circ$.
因为 $AC$ 是正方形 $ABCD$ 的对角线,
所以 $\angle ACB=\angle ACD=45^\circ $,
所以 $\angle ACF=\angle ACE$.
因为 $\angle EAF$ 被对角线 $AC$ 平分,
所以 $\angle CAF=\angle CAE$,
在 $\triangle ACF$ 和 $\triangle ACE$ 中,
$\begin{cases}\angle ACF=\angle ACE,\\AC=AC,\\\angle CAF=\angle CAE,\end{cases}$
所以 $\triangle ACF\cong \triangle ACE$,
所以 $CE=CF$.
因为 $CE=a$,$CF=b$,
所以 $a=b$.
因为 $\angle EAF=\angle DAC=45^\circ$,
所以 $\angle CAE=\angle DAE=\angle AEC=22.5^\circ$,
所以 $CE=CF=AC=4\sqrt 2$. -
当 $\triangle AEF$ 是直角三角形时,求 $a,b$ 的值;标注答案当 $\angle AEF=90^\circ $ 时,$a=4$,$b=8$;
当 $\angle AFE=90^\circ $ 时,$a=8$,$b=4$解析① 当 $\angle AEF=90^\circ $ 时,
因为 $\angle EAF=45^\circ $,
所以 $\angle AFE=45^\circ $,
所以 $\triangle AEF$ 是等腰直角三角形,
所以 $AF^2=2FE^2=2\left(CE^2+CF^2\right)$,
$AF^2=2\left(AD^2+BE^2\right)$,
所以 $2\left(CE^2+CF^2\right)=2\left(AD^2+BE^2\right)$,
所以 $CE^2+CF^2=AD^2+BE^2$,
所以 $CE^2+CF^2=16+\left(4+CE\right)^2$,
所以 $CF^2=8\left(CE+4\right)\quad \cdots \cdots ① $.
因为 $\angle AEB+\angle BEF=90^\circ $,$\angle AEB+\angle BAE=90^\circ $,
所以 $\angle BEF=\angle BAE$,
所以 $\triangle ABE\backsim \triangle ECF$,
所以 $\dfrac {AB} {CE} =\dfrac {BE} {CF} $,
所以 $\dfrac 4 {CE} =\dfrac {CE+4} {CF} $,
所以 $4CF=CE\left(CE+4\right)\quad \cdots \cdots ② $.
联立 ①② 得,$CE=4$,$CF=8$
所以 $a=4$,$b=8$.
② 当 $\angle AFE=90^\circ $ 时,
同 ① 的方法得,$CF=4$,$CE=8$,
所以 $a=8$,$b=4$. -
如图3,探索 $\angle EAF$ 绕点 $A$ 旋转的过程中 $a,b$ 满足的关系式,并说明理由.标注答案$ab=32$解析因为 $\angle BAG+\angle AGB=90^\circ $,$\angle AFC+\angle CGF=90^\circ $,$\angle AGB=\angle CGF$,
所以 $\angle BAG=\angle AFC$,
因为 $\angle BAC=45^\circ $,
所以 $\angle BAG+\angle CAF=45^\circ $,
所以 $\angle AFC+\angle CAF=45^\circ $,
因为 $\angle AFC+\angle AEC=180^\circ -\left(\angle CFE+\angle CEF\right)-\angle EAF=180^\circ -90^\circ -45^\circ =45^\circ $,
所以 $\angle CAF=\angle AEC$,
因为 $\angle ACF=\angle ACE=135^\circ $,
所以 $\triangle ACF\backsim \triangle ECA$,
所以 $\dfrac {AC} {EC} =\dfrac {CF} {AC} $,
所以 $EC\times CF=AC^2=2AB^2=32$,
所以 $ab=32$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3