如图，在 $\triangle ABC$ 中，$\angle BAC=\angle BCA=44^\circ$，$M$ 为 $\triangle ABC$ 形内一点，使得 $\angle MCA=30^\circ$，$\angle MAC=16^\circ$．求 $\angle BMC$ 的度数．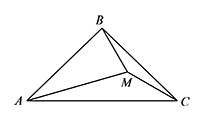
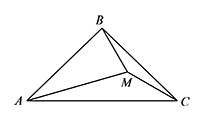
【难度】
【出处】
无
【标注】
【答案】
$\angle BMC=150^\circ$
【解析】
以 $AC$ 为边在 $\triangle ABC$ 同侧作等边 $\triangle ADC$，连接 $BD$．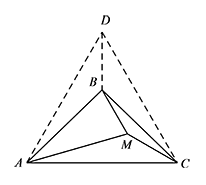
则 $\angle ADB=30^\circ=\angle ACM$，$\angle DAB=16^\circ=\angle MAC$．
所以 $\triangle DAB\cong \triangle CAM$．
则 $AB=AM$，$\angle ABM=76^\circ$，从而求得 $\angle BMC=150^\circ$．
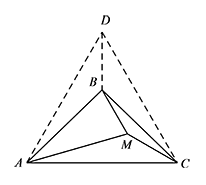则 $\angle ADB=30^\circ=\angle ACM$，$\angle DAB=16^\circ=\angle MAC$．所以 $\triangle DAB\cong \triangle CAM$．
则 $AB=AM$，$\angle ABM=76^\circ$，从而求得 $\angle BMC=150^\circ$．
答案
解析
备注
