如图,正方形 $ABCD$ 的对角线相交于点 $O$,点 $M$,$N$ 分别是边 $BC$,$CD$ 上的动点(不与点 $B$,$C$,$D$ 重合),$AM$,$AN$ 分别交 $BD$ 于点 $E$,$F$,且 $\angle MAN$ 始终保持 $45^\circ $ 不变.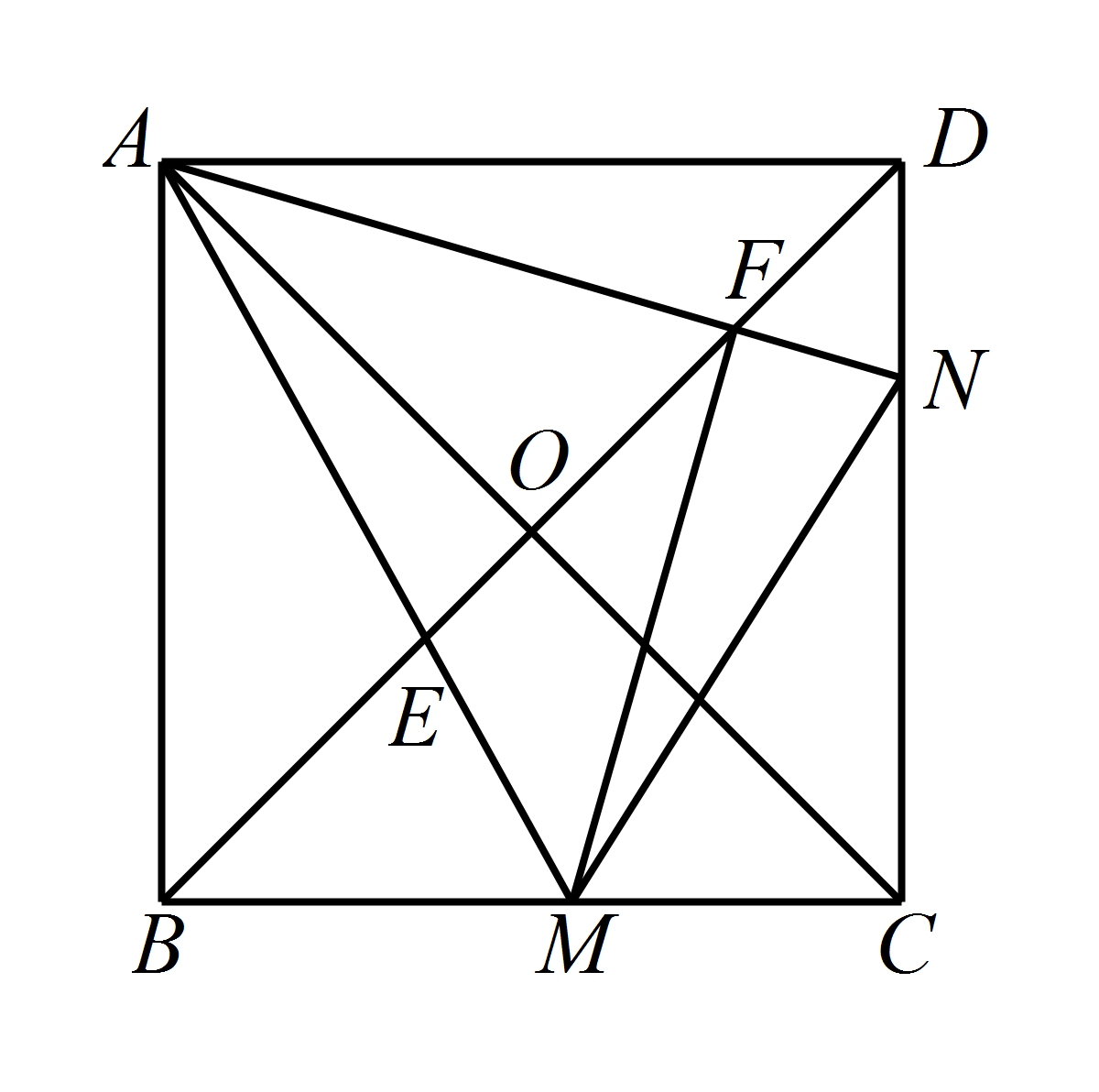

【难度】
【出处】
无
【标注】
-
求证:$\dfrac{AF}{AM }=\dfrac{\sqrt{2}}{2 }$;标注答案略解析因为四边形 $ABCD$ 是正方形,
所以 $\angle ABD=\angle CBD=45^\circ$,$\angle ABC=90^\circ$.
因为 $\angle MAN=45^\circ$,
所以 $\angle MAF=\angle MBE$,
所以 $A,B,M,F$ 四点共圆.
所以 $\angle ABM+\angle AFM=180^\circ $,
所以 $\angle AFM=90^\circ $,
所以 $\angle FAM=\angle FMA=45^\circ $,
所以 $AM=\sqrt{2}AF$,
所以 $\dfrac{AF}{AM }=\dfrac{\sqrt{2}}{2}$. -
求证:$AF\perp FM$;标注答案略解析由第1问可知 $\angle AFM=90^\circ $,
$\therefore AF\perp FM$. -
请探索:在 $\angle MAN$ 的旋转过程中,当 $\angle BAM$ 等于多少度时,$\angle FMN=\angle BAM$?写出你的探索结论,并加以证明.标注答案当 $\angle BAM=22.5^{\circ}$ 时,$\angle FMN=\angle BAM$解析因为 $A,B,M,F$ 四点共圆,
所以 $\angle BAM=\angle EFM$,
因为 $\angle BAM=\angle FMN$,
所以 $\angle EFM=\angle FMN$,
所以 $MN\parallel BD$,
所以 $\dfrac{CM}{CB}=\dfrac{CN}{CD}$,
因为 $CB=DC$,
所以 $CM=CN$,
所以 $MB=DN$,
在 $\triangle ABM$ 和 $\triangle ADN$ 中,
$\begin{cases}AB=AD,\\\angle ABM=\angle ADN=90^\circ ,\\BM=DN,\end{cases}$
所以 $\triangle ABM\cong \triangle ADN$,
所以 $\angle BAM=\angle DAN$,
因为 $\angle MAN=45^\circ $,
所以 $\angle BAM+\angle DAN=45^\circ $,
所以 $\angle BAM=22.5^\circ$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3