如图，在矩形纸片 $ABCD$ 中，已知 $AB=1$，$BC=\sqrt 3$，点 $E$ 在边 $CD$ 上移动，连接 $AE$，将多边形 $ABCE$ 沿直线 $AE$ 折叠，得到多边形 $AB'C'E$，点 $B,C$ 的对应点分别为点 $B',C'$．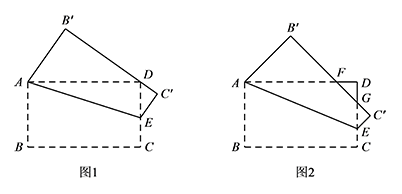
【难度】
【出处】
无
【标注】
-
当 $B'C'$ 恰好经过点 $D$ 时（如图1），求线段 $CE$ 的长；标注答案$CE=\sqrt 6-2$解析由翻折可得 $AB'=AB=1$，$B'C'=BC=\sqrt 3$，$C'E=CE$．
如图1，若点 $D$ 恰好在 $B'C'$ 上，
则在 $\mathrm{Rt}\triangle AB'D$ 中，$B'D=\sqrt{AD^2-AB'^2}=\sqrt 2$，
所以 $C'D=\sqrt 3-\sqrt 2$．
令 $CE=x$，则 $C'E=x$，$DE=1-x$．
在 $\mathrm{Rt}\triangle DC'E$ 中，有 $(\sqrt 3-\sqrt 2)^2+x^2=(1-x)^2$，
解得 $x=\sqrt 6-2$，即 $CE=\sqrt 6-2$． -
若 $B'C'$ 分别交 $AD,CD$ 于点 $F,G$，且 $\angle DAE=22.5^\circ$（如图2），求 $\triangle DFG$ 的面积；标注答案$S_{\triangle DFG}=\dfrac 52-\sqrt 6$解析如图2，若 $\angle DAE=22.5^\circ$，
则 $\angle DEA=\angle BAE=67.5^\circ$，$\angle AEC=112.5^\circ$．
由翻折可得 $\angle B'AE=\angle BAE=67.5^\circ$，$\angle AEC'=\angle AEC=112^\circ$，
所以 $\angle B'AF=45^\circ$，$\angle C'EG=45^\circ$．
所以 $\angle DFG=\angle B'FA=45^\circ=\angle C'GE=\angle DGF$，
即 $\triangle AB'F,\triangle FDG,\triangle EC'G$ 均为等腰直角三角形．
由 $AB'=AB=1$，可得 $AF=\sqrt 2$，
所以 $DG=DF=\sqrt 3-\sqrt 2$，
从而 $S_{\triangle DFG}=\dfrac 12(\sqrt 3-\sqrt 2)^2=\dfrac 52-\sqrt 6$． -
若点 $E$ 从点 $C$ 移动到点 $D$ 的过程中，求点 $C'$ 运动的路径长．标注答案$\dfrac 23\pi$解析当点 $E$ 和点 $D$ 重合时，四边形 $AB'C'E$ 的位置如图所示．
点 $C'$ 运动的轨迹为以点 $A$ 为圆心、$AC$ 为半径的 $\overparen{CC'}$．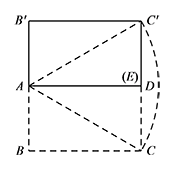
显然 $\tan\angle DAC=\dfrac{DC}{DA}=\dfrac{\sqrt 3}{3}$，$AC=2$．
所以 $\angle DAC'=\angle DAC=30^\circ$，
从而 $l_{\overparen{CC'}}=\dfrac{60^\circ}{360^\circ}\cdot 2\pi\cdot AC=\dfrac 23\pi$．
即 $C'$ 运动的路径长为 $\dfrac 23\pi$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
