如图1，在菱形 $ ABCD $ 中，$ AB=2 $，$ \angle BAD=60^\circ $，过点 $ D $ 作 $ DE\perp AB $ 于点 $ E $，$ DF\perp BC $ 于点 $ F $．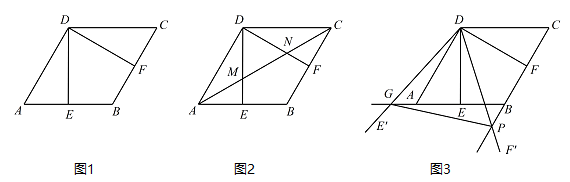
【难度】
【出处】
无
【标注】
-
如图2，连接 $ AC $ 分别交 $ DE $、$ DF $ 于点 $ M $，$ N $，求证：$ MN= \dfrac{1}{3}AC $；标注答案略解析如图，连接 $BD$，交 $AC$ 于点 $O$．
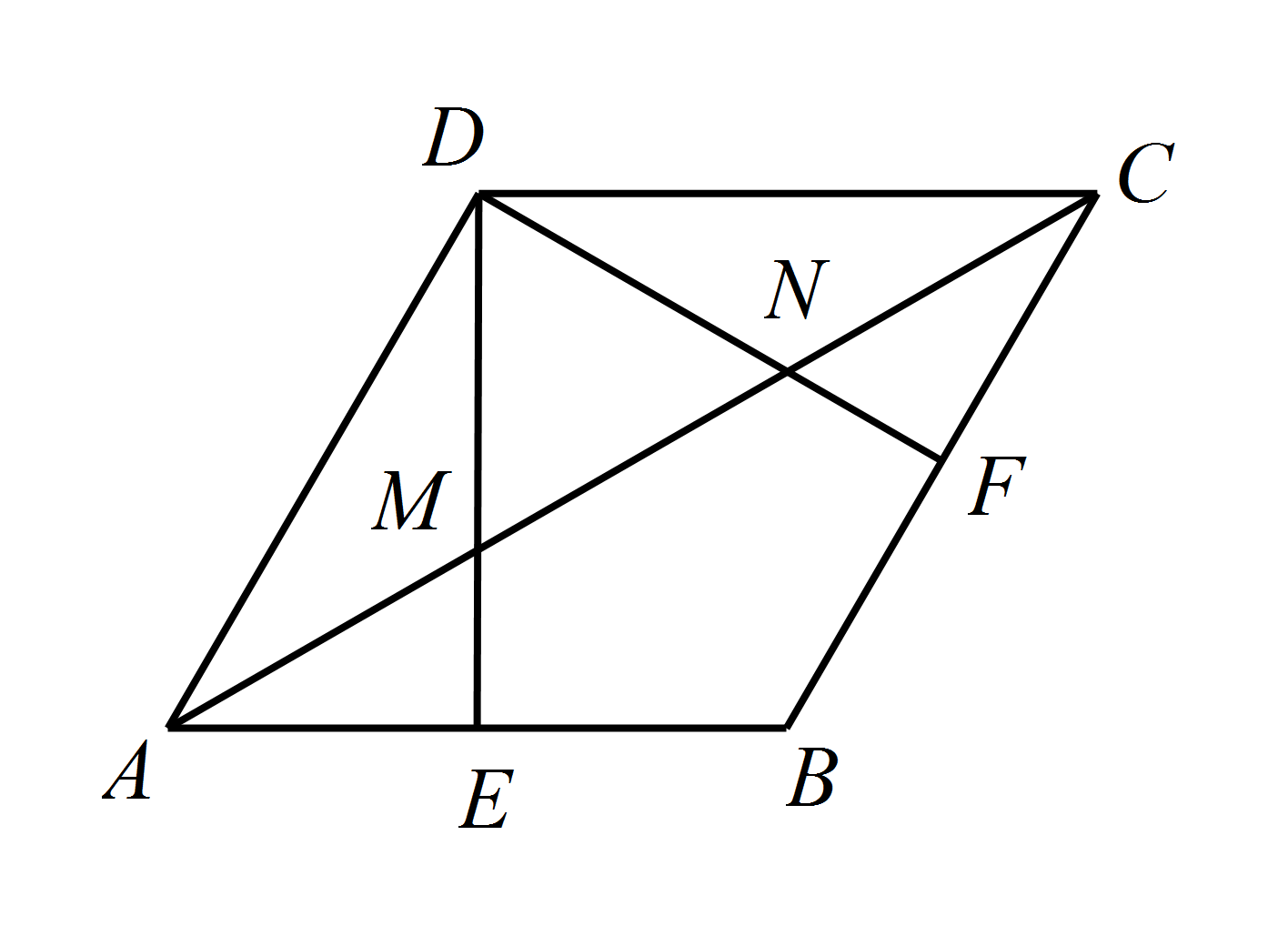在菱形 $ABCD$ 中，$\angle BAD=60^\circ$，$AD=AB$，
所以 $\triangle ABD$ 为等边三角形，
因为 $DE\perp AB$，
所以 $AE=EB$，
因为 $AB\parallel DC$，
所以 $\dfrac {AM} {MC} =\dfrac {AE} {DC} =\dfrac 1 2$，
同理可得 $\dfrac {CN} {AN} =\dfrac 1 2$，
所以 $MN=\dfrac 1 3 AC$． -
如图3，将 $ \triangle EDF $ 以点 $ D $ 为旋转中心旋转，其两边 $ DE' $，$ DF' $ 分别与直线 $ AB $，$ BC $ 相交于点 $ G $，$ P $，连接 $ GP $，当 $ \triangle DGP $ 的面积等于 $ 3\sqrt{3} $ 时，求旋转角的大小并指明旋转方向．标注答案将 $\triangle EDF$ 以点 $D$ 为旋转中心，顺时针或逆时针旋转 $60^\circ$ 时，$\triangle DGP$ 的面积等于 $3\sqrt{3}$解析因为 $ AB\parallel DC $，$ \angle BAD=60^\circ $，
所以 $ \angle ADC=120^\circ $，又 $ \angle ADE=\angle CDF=30^\circ $，
所以 $ \angle EDF=60^\circ $．
当 $ \angle EDF $ 顺时针旋转时，
由旋转的性质可知，$ \angle EDG=\angle FDP $，$ \angle GDP=\angle EDF=60^\circ $，
$ DE=DF=\sqrt{3} $，$ \angle DEG=\angle DFP=90^\circ $，
在 $ \triangle DEG $ 和 $ \triangle DFP $ 中，
$\begin{cases}\angle GDE=\angle PDF,\\\angle DEG=\angle DFP,\\DE=DF.\end{cases}$
所以 $ \triangle DEG \cong \triangle DFP$，
所以 $ DG=DP $，
所以 $ \triangle DGP $ 为等边三角形，
所以 $ \triangle DGP 的面积= \dfrac {\sqrt{3}} 4 DG^2=3\sqrt{3} $，
解得 $ DG=2\sqrt{3} $．
则 $ \cos\angle EDG=\dfrac {DE} {DG} =\dfrac 1 2 $，
所以 $ \angle EDG=60^\circ $，
所以当顺时针旋转 $ 60^\circ $ 时，$ \triangle DGP $ 的面积等于 $ 3\sqrt{3} $．
同理可得，当逆时针旋转 $ 60^\circ $ 时，$ \triangle DGP $ 的面积也等于 $ 3\sqrt{3} $，
综上所述，将 $ \triangle EDF $ 以点 $ D $ 为旋转中心，顺时针或逆时针旋转 $ 60^\circ $ 时，$ \triangle DGP $ 的面积等于 $ 3\sqrt{3} $．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
