将一个直角三角形纸片 $ABO$ 放置在平面直角坐标系中，点 $A(\sqrt 3,0)$，点 $B(0,1)$，点 $O(0,0)$．$P$ 是边 $AB$ 上的一点（点 $P$ 不与点 $A,B$ 重合），沿着 $OP$ 折叠该纸片，得点 $A$ 的对应点 $A'$．
【难度】
【出处】
无
【标注】
-
如图1，当点 $A'$ 在第一象限，且满足 $A'B\perp OB$ 时，求点 $A'$ 的坐标；标注答案$(\sqrt 2,1)$解析根据题意可得 $OA=\sqrt 3$，$OB=1$．
由翻折可得 $OA'=OA=\sqrt 3$．
而 $A'B\perp OB$，所以 $A'B=\sqrt{OA'^2-OB^2}=\sqrt 2$，
所以点 $A'$ 的坐标为 $(\sqrt 2,1)$． -
如图2，当 $P$ 为 $AB$ 中点时，求 $A'B$ 的长；标注答案$A'B=1$解析因为点 $P$ 为 $AB$ 中点，
所以 $OP=\dfrac 12 AB=BP=AP$．
而 $\tan \angle ABO=\sqrt 3$，所以 $\angle ABO=60^\circ$．
所以 $\triangle OBP$ 为等边三角形，
所以 $\angle BPO=60^\circ$，$\angle APO=120^\circ$．
由翻折可得 $\angle A'PO=\angle APO=120^\circ$，$A'P=AP=BP$，
所以 $\angle A'PB=60^\circ$，即 $\triangle A'BP$ 也为等边三角形．
所以 $A'B=PB=OB=1$． -
当 $\angle BPA'=30^\circ$ 时，求点 $P$ 的坐标．标注答案点 $P$ 的坐标为 $\left(\dfrac{3-\sqrt 3}2,\dfrac{3-\sqrt 3}2\right)$ 或 $\left(\dfrac{2\sqrt 3-3}2,\dfrac{\sqrt 3}2\right)$解析① 当点 $A'$ 在 $AB$ 上方时，如图．
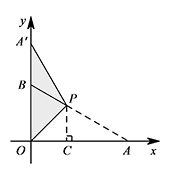此时 $\angle APA'=150^\circ$．
由翻折可得 $\angle APO=\angle A'PO=\dfrac 12(360^\circ-\angle APA')=105^\circ$，
所以 $\angle AOP=45^\circ$．
过点 $P$ 作 $PC\perp x$ 轴于点 $C$．
令 $OC=x$，则 $PC=x$，$AC=\sqrt 3x$，
所以 $OA=x+\sqrt 3x=\sqrt 3$，解得 $x=\dfrac{3-\sqrt 3}2$．
所以此时点 $P$ 的坐标为 $\left(\dfrac{3-\sqrt 3}2,\dfrac{3-\sqrt 3}2\right)$；
② 当点 $A'$ 在 $AB$ 下方时，如图．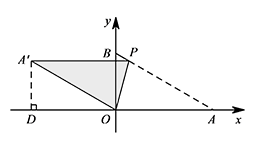
此时 $\angle BPA'=\angle BAO=30^\circ$，
所以 $A'P\parallel OA$．
过点 $A'$ 作 $A'\perp x$ 轴于点 $D$，则 $\angle A'OD=\angle PA'O$．
由翻折可得 $OA'=OA=\sqrt 3$，$\angle PA'O=\angle PAO=30^\circ$，
所以 $A'D=\dfrac 12OA'=\dfrac{\sqrt 3}2$，$OD=\sqrt 3A'D=\dfrac 32$．
同样由翻折可得 $A'P=AP$，$\angle A'PO=\angle APO$，
所以 $\angle AOP=\angle A'PO=\angle APO$，
从而 $AP'=AP=AO=\sqrt 3$．
所以此时点 $P$ 的坐标为 $\left(\dfrac{2\sqrt 3-3}2,\dfrac{\sqrt 3}2\right)$．
综上所述，点 $P$ 的坐标为 $\left(\dfrac{3-\sqrt 3}2,\dfrac{3-\sqrt 3}2\right)$ 或 $\left(\dfrac{2\sqrt 3-3}2,\dfrac{\sqrt 3}2\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
