已知四边形 $ABCD$ 是菱形，$AB=4$，$\angle ABC=60^\circ$，$\angle EAF$ 的两边分别与射线 $CB,DC$ 相交于点 $E,F$，且 $\angle EAF=60^\circ$．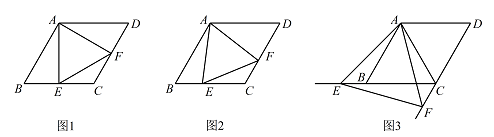
【难度】
【出处】
无
【标注】
-
如图 1，当点 $E$ 是线段 $CB$ 的中点时，直接写出线段 $AE,EF$，$AF$ 之间的数量关系；标注答案$AE=EF=AF$解析如图 1 中，连接 $AC$．
因为四边形 $ABCD$ 是菱形，$\angle B=60^\circ$，
所以 $AB=BC=CD=AD$，$\angle B=\angle D=60^\circ$．
所以 $\triangle ABC$，$\triangle ADC$ 是等边三角形．
所以 $\angle BAC=\angle DAC=60^\circ$．
因为 $BE=EC$，
所以 $\angle BAE=\angle CAE=30^\circ$，$AE\perp BC$．
因为 $\angle EAF=60^\circ$，
所以 $\angle CAF=\angle DAF=30^\circ$．
所以 $AF\perp CD$．
所以 $AE=AF$（菱形的高相等）．
所以 $\triangle AEF$ 是等边三角形．
所以 $AE=EF=AF$． -
如图 2，当点 $E$ 是线段 $CB$ 上任意一点时（点 $E$ 不与 $B,C$ 重合），求证：$BE=CF$；标注答案略解析如图 2 中，连接 $AC$．
因为 $\angle BAC=\angle EAF=60^{\circ}$，
所以 $ \angle BAE=\angle CAE$．
在 $\triangle BAE$ 和 $\triangle CAF$ 中，
$\begin{cases}\angle BAE=\angle CAE,\\BA=AC,\\\angle B=\angle ACF,\end{cases}$
所以 $ \triangle BAE\cong\triangle CAF$．
所以 $ BE=CF$． -
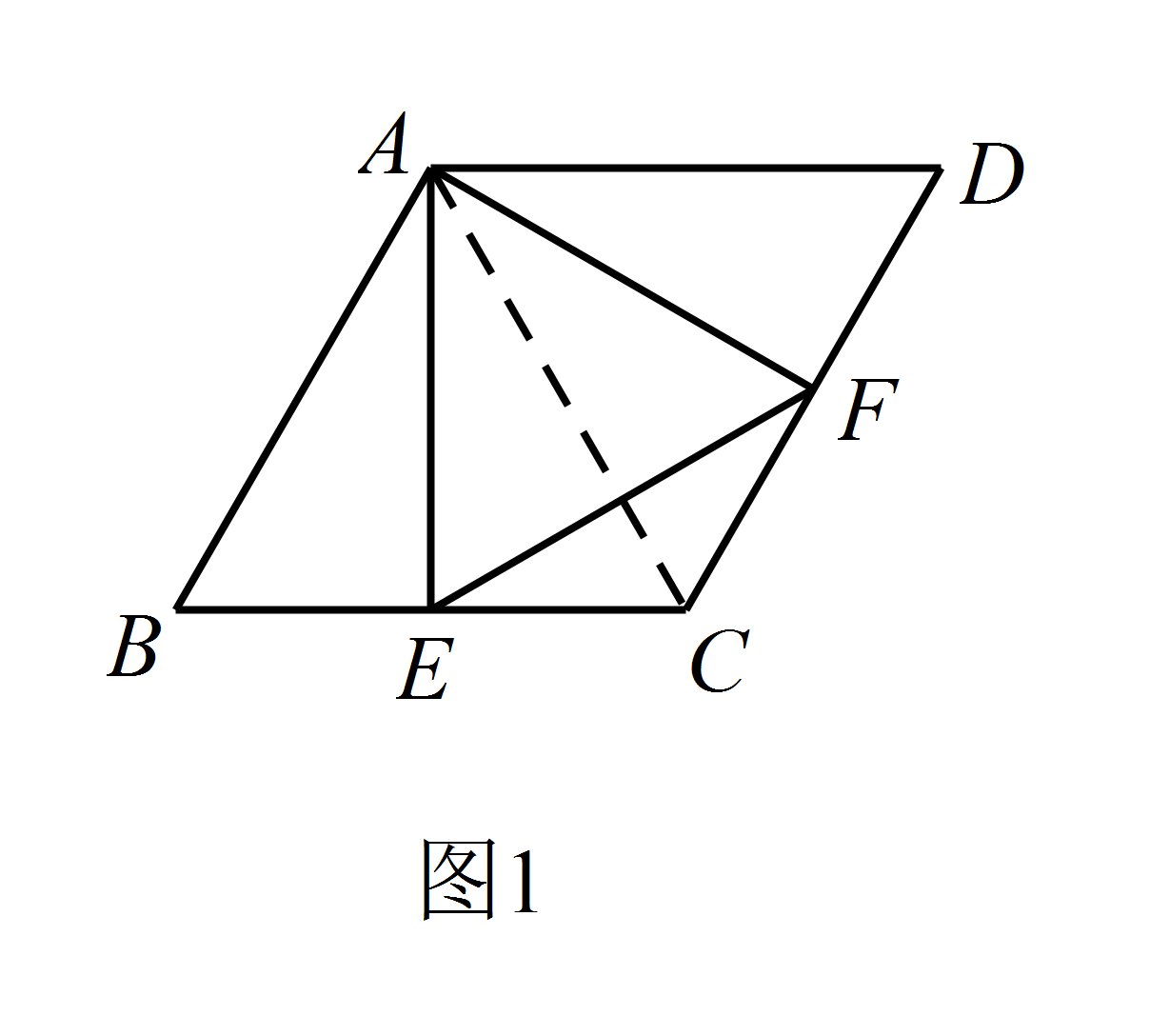
如图 3，当点 $E$ 在线段 $CB$ 的延长线上，且 $\angle EAB=15^{\circ}$ 时，求点 $F$ 到 $BC$ 的距离．标注答案点 $F$ 到 $BC$ 的距离为 $3-\sqrt{3}$解析过点 $A$ 作 $AG\perp BC$ 于点 $G$，过点 $F$ 作 $FH\perp EC$ 于点 $H$．
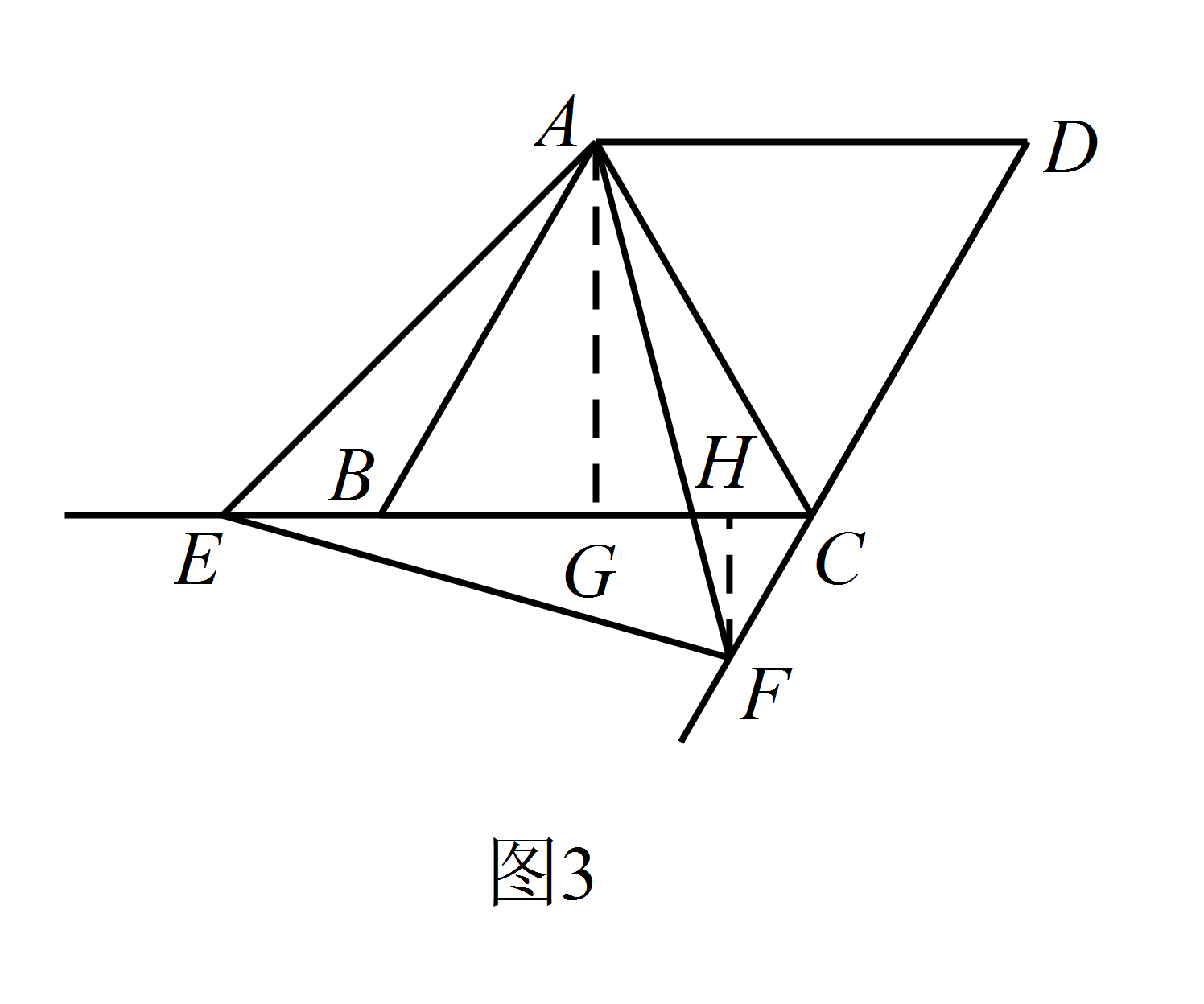因为 $\angle EAB=15^\circ$，$\angle ABC=60^\circ$，
所以 $ \angle AEB=45^\circ$．
在 ${\mathrm {Rt}}\triangle AGB$ 中，$\angle ABC=60^\circ$，$AB=4$，
所以 $ BG=2$，$AG=2\sqrt{3}$．
在 ${\mathrm {Rt}}\triangle AEG$ 中，$\angle AEG=\angle EAG=45^\circ$，
所以 $ AG=GE=2\sqrt{3}$．
所以 $ EB=EG-BG=2\sqrt{3}-2$．
因为 $\triangle AEB\cong\triangle AFC$，
所以 $ AE=AF$，$EB=CF=2\sqrt{3}-2$，$\angle AEB=\angle AFC=45^\circ$．
因为 $\angle EAF=60^\circ$，$AE=AF$，
所以 $ \triangle AEF$ 是等边三角形．
所以 $ \angle AEF=\angle AFE=60^\circ$．
因为 $\angle AEB=45^\circ$，$\angle AEF=60^\circ$，
所以 $ \angle CEF=\angle AEF-\angle AEB=15^\circ$．
在 ${\mathrm {Rt}}\triangle EFH$ 中，$\angle CEF=15^\circ$，
所以 $ \angle EFH=75^\circ$．
因为 $\angle AFE=60^\circ$，
所以 $ \angle AFH=\angle EFH-\angle AFE=15^\circ$．
因为 $\angle AFC=45^\circ$，$\angle CFH=\angle AFC-\angle AFH=30^\circ$，
在 ${\mathrm {Rt}}\triangle CHF$ 中，$\angle CFH=30^\circ$，$CF=2\sqrt{3}-2$，
所以 $ FH=CF\cdot \cos30^\circ=\left(2\sqrt{3}-2\right)\cdot \dfrac{\sqrt{3}}2=3-\sqrt{3}$．
所以 点 $F$ 到 $BC$ 的距离为 $3-\sqrt{3}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
