在学习了图形的旋转知识后，数学兴趣小组的同学们又进一步对图形旋转前后的线段之间、角之间的关系进行了探究．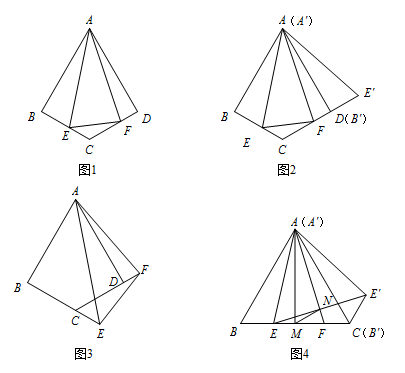
【难度】
【出处】
无
【标注】
-
【尝试探究】
如图1，在四边形 $ABCD$ 中，$AB=AD$，$\angle BAD=60^\circ$，$\angle ABC=\angle ADC=90^\circ$，点 $E,F$ 分別在线段 $BC,CD$ 上，$\angle EAF=30^\circ$，连接 $EF$．
（i）如图2，将 $\triangle ABE$ 绕点 $A$ 逆时针旋转 $60^\circ$ 后得到 $\triangle A'B'E'$（$A'B'$ 与 $AD$ 重合），请直接写出 $\angle E'AF=$
（ii）如图3，当点 $E,F$ 分别在线段 $BC,CD$ 的延长线上时，其他条件不变，请探究线段 $BE,EF,FD$ 之间的数量关系，并说明理由．标注答案（i）在图2中，$\angle E'AF=30^\circ$，$EF=BE+FD$；
（ii）在图3中，线段 $BE,EF,FD$ 之间的数量关系为 $EF=BE-FD$解析（i）因为将 $\triangle ABE$ 绕点 $A$ 逆时针旋转 $60^\circ$ 得到 $\triangle A'B'E'$，
所以 $AE'=AE$，$\angle A'B'E'=\angle B=90^\circ$，$B'E'=BE$，$\angle B'A'E'=\angle BAE$．
因为 $\angle ADC=90^\circ$，
所以 $\angle ADC+\angle A'B'E'=180^\circ$．
所以 $F$、$D$、$E'$ 在同一条直线上．
因为 $\angle BAD=60^\circ$，$\angle EAF=30^\circ$，
所以 $\angle BAE+\angle FAD=30^\circ$．
所以 $\angle B'A'E'+\angle FAD=30^\circ$．
所以 $\angle E'AF=\angle FAE=30^\circ$．
又因为 $AE'=AE$，$AF=AF$，
所以 $\triangle AFE\cong \triangle AFE'$．
所以 $EF=E'F=DF+DE'=DF+BE$．
（ii）如答案图1，将 $\triangle ABE$ 绕点 $A$ 逆时针旋转 $60^\circ$ 后得到 $\triangle A'B'E'$（$A'B'$ 与 $AD$ 重合）．
因为将 $\triangle ABE$ 绕点 $A$ 逆时针旋转 $60^\circ$ 得到 $\triangle A'B'E'$，
所以 $AE'=AE$，$\angle A'B'E'=\angle B=90^\circ$，$B'E'=BE$，$\angle B'A'E'=\angle BAE$．
因为 $\angle ADC=90^\circ$，
所以 $\angle ADC+\angle A'B'E'=180^\circ$．
所以 $F$、$D$、$E'$ 在同一条直线上．
因为 $\angle BAE+\angle EAD=60^\circ$，$\angle B'A'E'=\angle BAE$，
所以 $\angle B'A'E'+\angle EAD=60^\circ$．
即 $\angle E'AE=60^\circ$．
又因为 $\angle EAF=30^\circ$，
所以 $\angle E'AF=\angle E'AE-\angle EAF=60^\circ-30^\circ=30^\circ$．
所以 $\angle EAF=\angle E'AF$．
又因为 $AE'=AE$，$AF=AF$，
所以 $\triangle AFE\cong \triangle AFE'$．
所以 $EF=E'F=DE'-DF=BE-DF$． -
【拓展延伸】
如图4，在等边 $\triangle ABC$ 中，$E$、$F$ 是边 $BC$ 上的两点，$\angle EAF=30^\circ$，$BE=1$，将 $\triangle ABE$ 绕点 $A$ 逆时针旋转 $60^\circ$ 得到 $\triangle A'B'E'$（$A'B'$ 与 $AC$ 重合），连接 $EE'$，$AF$ 与 $EE'$ 交于点 $N$，过点 $A$ 作 $AM\perp BC$ 于点 $M$，连接 $MN$，求线段 $MN$ 的长度．标注答案$MN=\dfrac{\sqrt{3}}{2}$解析如答案图2，连接 $E'F$．
因为将 $\triangle ABE$ 绕点 $A$ 逆时针旋转 $60^\circ$ 得到 $\triangle A'B'E'$（$A'B'$ 与 $AC$ 重合）．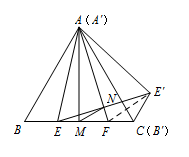
所以 $AE'=AE$，$ B'E'=BE=1$，$\angle B'A'E'=\angle BAE$．
因为 $\angle BAE+\angle EAC=60^\circ$，$\angle B'A'E'=\angle BAE$，
所以 $\angle B'A'E'+\angle EAC=60^\circ$．
即 $\angle E'AE=60^\circ$．
又因为 $AE'=AE$，
所以 $\triangle EAE'$ 是等边三角形．
因为 $\angle E'AE=60^\circ$，$\angle EAF=30^\circ$，
所以 $\angle E'AF=\angle EAF=30^\circ$．
又因为 $AE'=AE$，
所以 $AN\perp EE'$（三线合一）．
所以 $\dfrac{AN}{AE'}=\dfrac{\sqrt 3}{2}$．
在等边 $\triangle ABC$ 中，因为 $AM\perp BC$ 于点 $M$，
所以 $\dfrac{AM}{AC}=\dfrac{\sqrt{3}}{2}$，且 $\angle CAM=\angle BAM=\dfrac12\angle BAC=30^\circ$．
可证 $\angle E'AF=\angle EAF=30^\circ$．
所以 $\angle E'AF=\angle CAM=30^\circ$．
所以 $\angle E'AF-\angle FAC=\angle CAM-\angle FAC$．
所以 $\angle E'AC=\angle FAM$．
又因为 $\dfrac{AN}{AE'}=\dfrac{\sqrt{3}}{2}$，$\dfrac{AM}{AC}=\dfrac{\sqrt{3}}{2}$，
所以 $\triangle MAN\backsim \triangle CAE'$．
所以 $\dfrac{MN}{CE'}=\dfrac{\sqrt{3}}{2}$．
又因为 $CE'=1$，
所以 $MN=\dfrac{\sqrt{3}}{2}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
