如图1，在正方形 $ABCD$ 内作 $\angle EAF=45^\circ$，$AE$ 交 $BC$ 于点 $E$，$AF$ 交 $CD$ 于点 $F$，连接 $EF$，过点 $A$ 作 $AH\perp EF$，垂足为 $H$．
【难度】
【出处】
无
【标注】
-
如图2，将 $\triangle ADF$ 绕点 $A$ 顺时针旋转 $90^\circ$ 得到 $\triangle ABG$．
（i）求证：$\triangle AGE\cong \triangle AFE$；
（ii）若 $BE=2$，$DF=3$，求 $AH$ 的长．标注答案（ii）$AH=6$解析（i）由旋转的性质可知 $AF=AG$，$\angle DAF=\angle BAG$．
因为四边形 $ABCD$ 为正方形，
所以 $\angle BAD=90^\circ$．
又因为 $\angle EAF=45^\circ$，
所以 $\angle BAE+\angle DAF=45^\circ$．
所以 $\angle BAG+\angle BAE=45^\circ$．
所以 $\angle GAE=\angle FAE$．
在 $\triangle GAE$ 和 $\triangle FAE$ 中，
所以 $\triangle GAE\cong \triangle FAE$．
（ii）因为 $\triangle GAE\cong \triangle FAE$，$AB\perp GE$，$AH\perp EF$，
所以 $AB=AH$，$GE=EF=5$．
设正方形的边长为 $x$，则 $EC=x-2$，$FC=x-3$．
在 $\mathrm {Rt}\triangle EFC$ 中，由勾股定理得 $EF^2=FC^2+EC^2$，
即 $(x-2)^2+(x-3)^2=25$，解得 $x=6$．
所以 $AH=AB=6$． -
如图3，连接 $BD$ 交 $AE$ 于点 $M$，交 $AF$ 于点 $N$．请探究并猜想：线段 $BM$，$MN$，$ND$ 之间有什么数量关系？并说明理由．标注答案$MN^2=ND^2+BM^2$解析如图所示，将 $\triangle ABM$ 逆时针旋转 $90^\circ$ 得 $\triangle ADM'$．
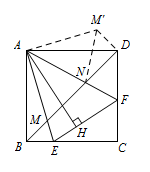因为四边形 $ABCD$ 为正方形，
所以 $\angle ABD=\angle ADB=45^\circ$．
由旋转的性质可知：$\angle ABM=\angle ADM'=45^\circ$，$BE=DM'$．
所以 $\angle NDM'=90^\circ$．
所以 $NM'^2=ND^2+DM'^2$．
因为 $\angle EAM'=90^\circ$，$\angle EAF=45^\circ$，
所以 $\angle EAF=\angle FAM'=45^\circ$．
在 $\triangle AMN$ 和 $\triangle ANM'$ 中，
$\begin{cases}AM=AM',\\ \angle MAN=\angle M'AN,\\ AN=AN.\end{cases}$
所以 $\triangle AMN\cong \triangle ANM'$．
所以 $MN=NM'$．
又因为 $BM=DM'$，
所以 $MN^2=ND^2+BM^2$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
