如图 1,在正方形 $ABCD$ 中,$P$ 是对角线 $BD$ 上的一点,点 $E$ 在 $AD$ 的延长线上,且 $PA=PE$,$PE$ 交 $CD$ 于 $F$.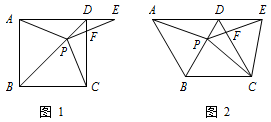

【难度】
【出处】
无
【标注】
-
证明:$PC=PE$;标注答案略解析因为点 $P$ 在对角线 $BD$ 上,
由正方形的轴对称性,可得 $PA=PC$,
而 $PA=PE$,
所以 $PC=PE$. -
求 $\angle CPE$ 的度数;标注答案$\angle CPE=90^\circ$解析同样由正方形的轴对称性,可得 $\angle PAD=\angle PCD$.
因为 $PA=PE$,
所以 $\angle E=\angle PAD=\angle PCD$,
从而 $D,P,C,E$ 四点共圆,
所以 $\angle CPE=\angle CDE=90^\circ$. -
如图 2,把正方形 $ABCD$ 改为菱形 $ABCD$,其他条件不变,当 $\angle ABC=120^\circ $ 时,连接 $CE$,试探究线段 $AP$ 与线段 $CE$ 的数量关系,并说明理由.标注答案$AP=CE$解析由菱形的轴对称性,可得 $PA=PC$,$\angle PAD=\angle PCD$.
因为 $PA=PE$,
所以 $PC=\angle PE$,$\angle DEP=\angle DAP=\angle DCP$,
从而 $D,P,C,E$ 四点共圆,
所以 $\angle EPC=\angle EDC=60^\circ$,
即 $\triangle EPC$ 为等边三角形,
所以 $AP=CE$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3