如图，矩形 $ABCD$ 中，$AB=4$，$AD=3$，$M$ 是边 $CD$ 上一点，将 $\triangle ADM$ 沿 $AM$ 对折得到 $\triangle ANM$，当射线 $BN$ 交线段 $CD$ 于点 $F$ 时，求 $DF$ 的最大值．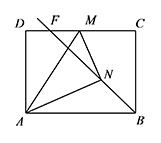
【难度】
【出处】
无
【标注】
【答案】
$4-\sqrt 7$
【解析】
如图，过点 $A$ 作 $AH\perp BF$ 于点 $H$．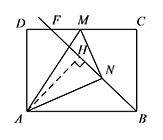
则 $\triangle ABH\backsim \triangle BFC$，
所以 $\dfrac{BC}{FC}=\dfrac{AH}{BH}$，
从而 $\dfrac{FC^2}{BC^2}=\dfrac{AB^2-AH^2}{AH^2}=\dfrac{AB^2}{AH^2}-1$．
欲使 $DF$ 最大，需使 $CF$ 最小，即 $AH$ 最大即可，
而 $AH\leqslant AN$，
所以当 $N,H$ 重合时，$DF$ 取得最大值，而此时 $M,F$ 也重合，如图．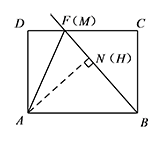
因为 $AN=AD=BC$，
所以 $\triangle ABN\cong \triangle BFC$，
所以 $BF=AB=4$，
从而 $CF=\sqrt 7$，$DF=4-\sqrt 7$．
即 $DF$ 的最大值为 $4-\sqrt 7$．
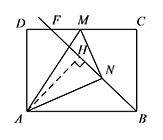则 $\triangle ABH\backsim \triangle BFC$，所以 $\dfrac{BC}{FC}=\dfrac{AH}{BH}$，
从而 $\dfrac{FC^2}{BC^2}=\dfrac{AB^2-AH^2}{AH^2}=\dfrac{AB^2}{AH^2}-1$．
欲使 $DF$ 最大，需使 $CF$ 最小，即 $AH$ 最大即可，
而 $AH\leqslant AN$，
所以当 $N,H$ 重合时，$DF$ 取得最大值，而此时 $M,F$ 也重合，如图．
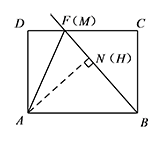因为 $AN=AD=BC$，所以 $\triangle ABN\cong \triangle BFC$，
所以 $BF=AB=4$，
从而 $CF=\sqrt 7$，$DF=4-\sqrt 7$．
即 $DF$ 的最大值为 $4-\sqrt 7$．
答案
解析
备注
