设 $\triangle {ABC}$ 的外心、内心分别为 $O$,$I$,$\angle A$,$\angle B$,$\angle C$ 内的旁心分别为 $I_1$,$I_2$,$I_3$,证明: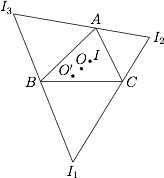

【难度】
【出处】
2010年全国高中数学联赛天津市预赛
【标注】
-
$\triangle {I_1I_2I_3}$ 为锐角三角形;标注答案略解析因为$$\angle I_3I_1I_2=90^{\circ}-\dfrac {\angle A}{2}<90^{\circ},$$所以 $\angle I_3I_1I_2$ 为锐角.
同理可得 $\angle I_1I_2I_3$,$\angle I_2I_3I_1$ 也为锐角,因此 $\triangle I_1I_2I_3 $ 为锐角三角形. -
若 $\triangle {I_1I_2I_3}$ 的外心为 $O'$,则 $O'$、$O$、$I$ 三点共线.标注答案略解析设 $AI_1$,$BI_2$,$CI_3$ 分别与圆 $O$ 相交于点 $D$,$E$,$F$,则 $D$,$E$,$F$ 分别为 $II_1$,$II_2$,$II_3$ 的中点,所以 $I$ 为 $\triangle DEF $ 与 $\triangle I_1I_2I_3 $ 的位似中心,且位似比为 $2$.
又因为 $\triangle DEF $ 的外心就是 $\triangle ABC$ 的外心,因此 $O'$,$O$,$I$ 三点共线,且 $O$ 为 $IO'$ 的中点.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2