在菱形 $ABCD$ 中，$\angle ADC=120^\circ$，点 $E$ 是对角线 $AC$ 上一点，连接 $DE$，$\angle DEC=50^\circ$，将线段 $BC$ 绕点 $B$ 逆时针旋转 $50^\circ$ 并延长得到射线 $BF$，交 $ED$ 的延长线于点 $G$．求证：$EG=BC$．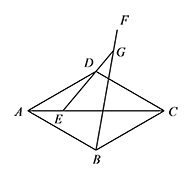
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
连接 $BE$，如图．
因为四边形 $ABCD$ 是菱形，
所以 $AD\parallel BC$．
因为 $\angle ADC=120^\circ$，
所以 $\angle DCB=60^\circ$．
因为 $AC$ 是菱形 $ABCD$ 的对角线，
所以 $\angle DCA=\dfrac12\angle DCB=30^\circ$，
所以 $\angle EDC=180^\circ-\angle DEC-\angle DCA=100^\circ$．
由菱形的对称性可知 $\angle BEC=\angle DEC=50^\circ$，$\angle EBC=\angle EDC=100^\circ$．
所以 $\angle GEB=\angle DEC+\angle BEC=100^\circ$，
所以 $\angle GEB=\angle CBE$．
因为 $\angle FBC=50^\circ$，
所以 $\angle EBG=\angle EBC-\angle FBC=50^\circ=\angle BEC$．
所以 $\triangle GEB\cong\triangle CBE$，
所以 $EG=BC$．
因为四边形 $ABCD$ 是菱形，所以 $AD\parallel BC$．
因为 $\angle ADC=120^\circ$，
所以 $\angle DCB=60^\circ$．
因为 $AC$ 是菱形 $ABCD$ 的对角线，
所以 $\angle DCA=\dfrac12\angle DCB=30^\circ$，
所以 $\angle EDC=180^\circ-\angle DEC-\angle DCA=100^\circ$．
由菱形的对称性可知 $\angle BEC=\angle DEC=50^\circ$，$\angle EBC=\angle EDC=100^\circ$．
所以 $\angle GEB=\angle DEC+\angle BEC=100^\circ$，
所以 $\angle GEB=\angle CBE$．
因为 $\angle FBC=50^\circ$，
所以 $\angle EBG=\angle EBC-\angle FBC=50^\circ=\angle BEC$．
所以 $\triangle GEB\cong\triangle CBE$，
所以 $EG=BC$．
答案
解析
备注
