在正方形 $ABCD$ 外侧作直线 $AP$，点 $B$ 关于直线 $AP$ 的对称点为 $E$，连接 $BE,DE$，其中 $DE$ 交直线 $AP$ 于点 $F$．
【难度】
【出处】
无
【标注】
-
如图1，若 $\angle PAB=20^\circ$，求 $\angle ADF$ 的度数；标注答案$\angle ADF=25^\circ$解析连接 $AE$，
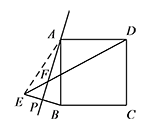因为四边形 $ABCD$ 是正方形，所以 $\angle BAD=90^\circ$．
则 $\angle PAB=\angle PAE=20^\circ$，$AE=AB=AD$．
所以 $\angle EAD=130^\circ$，所以 $\angle ADF=25^\circ$． -
如图2，若 $45^\circ<\angle PAB<90^\circ$，用等式表示线段 $AB,FE,FD$ 之间的数量关系，并证明．标注答案$EF^2+FD^2=2AB^2$解析连接 $AE,BF,BD$．
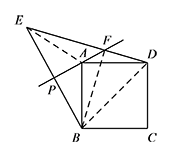由轴对称的性质可得 $EF=BF$，$AE=AB=AD$，$\angle ABF=\angle AEF=\angle ADF$，
所以 $\angle BFD=\angle BAD=90^\circ$，
所以 $BF^2+FD^2=BD^2$，
所以 $EF^2+FD^2=2AB^2$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
