正方形 $ABCD$ 内部有一点 $P$,使得 $\triangle PBC$ 为等边三角形,作点 $C$ 关于 $AP$ 的对称点 $C'$,连接 $PC',DC',AC',CC'$ 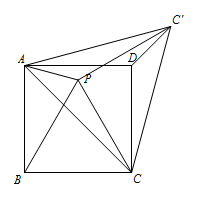

【难度】
【出处】
无
【标注】
-
求出 $\angle APC'$ 的度数;标注答案$\angle APC'=135^\circ$解析因为 $\angle PCB=\angle PBC=60^circ,PB=BC$,
所以 $AB=PB,\angle ABP=30^\circ,\angle ACP=15^\circ$,
所以 $\angle BAP=75^\circ,\angle PAC=30^\circ$,
所以 $\angle APC=180^\circ-\angle PAC-\angle ACP=135^\circ$,
因为 $C,C'$ 关于 $AP$ 对称,
所以 $\angle APC'=\angle APC=135^\circ$. -
求出 $\angle PC'D$ 的度数.标注答案$\angle PC'D=15^\circ$解析因为 $AC'=AC,\angle CAP=\angle C'AP=30^\circ$,
所以 $\angle CAC'=60^\circ$,
所以 $\triangle CAC'$ 为等边三角形,
因为 $AC'=CC=,AD=CD,C'D=C'D$,
所以 $\triangle AC'D\cong \triangle CC'D$,
所以 $\angle AC'D=\angle CC'D=\dfrac 12\angle AC'C=30^\circ$,
因为 $\angle AC'P=\angle ACP=15^\circ$,
所以 $\angle PC'D=15^\circ$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2