如图，在矩形 $OABC$ 中，$OA=3$，$ OC=5 $，分别以 $OA,OC$ 所在直线为 $x,y$ 轴，建立平面直角坐标系，$D$ 是边 $CB$ 上的一个动点（不与 $C,B$ 重合），反比例函数 $y=kx\left(k
> 0\right)$ 的图象经过点 $D$ 且与边 $BA$ 交于点 $E$，连接 $DE$．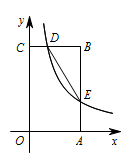
> 0\right)$ 的图象经过点 $D$ 且与边 $BA$ 交于点 $E$，连接 $DE$．
【难度】
【出处】
无
【标注】
-
连接 $CA$，判断 $DE$ 与 $CA$ 是否平行？请说明理由；标注答案$DE\parallel AC$解析如图，设点 $D$ 的坐标为 $\left(x,5\right)$，点 $E$ 的坐标为 $\left(3,\dfrac 53x\right)$．
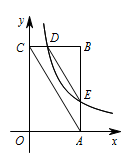则 $BD=3-x$，$BE=5-\dfrac 53x$，
所以 $\dfrac{BD}{BE}=\dfrac{3-x}{5-\dfrac 53x}=\dfrac 35=\dfrac{BC}{BA}$，
即 $\dfrac{BD}{BC}=\dfrac{BE}{BA}$，
所以 $DE\parallel AC$． -
是否存在点 $D$，使得点 $B$ 关于 $DE$ 的对称点在 $OC$ 上？若存在，求出点 $D$ 的坐标；若不存在，请说明理由．标注答案$D\left(\dfrac{48}{50},5\right)$解析若存在满足条件的点 $D$，则点 $B$ 关于 $DE$ 的对称点 $B'$ 在 $OC$ 上，连接 $B'D,B'E$．
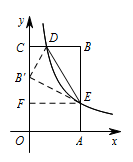设点 $D$ 的坐标为 $\left(x,5\right)$，点 $E$ 的坐标为 $\left(3,\dfrac 53x\right)$．
则 $CD=x$，$B'D=BD=3-x$，$AE=\dfrac 53x$，$B'E=BE=5-\dfrac 53x$．
如图，作 $EF\perp OC$，垂足为点 $F$，则 $EF=BC=3$，$OF=AE=\dfrac 53x$．
易证 $\triangle B'CD \backsim \triangle EFB'$，
所以 $\dfrac {B'E}{DB'}=\dfrac {B'F}{DC}=\dfrac{EF}{B'C}$，
即 $\dfrac {5-\dfrac 53x }{3-x}=\dfrac {B'F}{x}=\dfrac 3{B'C}$，
得到 $B'F=\dfrac 53x$，$B'C=\dfrac 95$．
由 $OF+B'F+B'C=OC$，得 $\dfrac 53x+\dfrac 53x+\dfrac 95=5$，
解得 $x=\dfrac{48}{50}$．
所以存在满足条件的点 $D$，其坐标为 $D\left(\dfrac{48}{50},5\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
