查看数据源：5928d51eeab1df0008257220
如图，在平面直角坐标系中，矩形 $OABC$ 的顶点 $A$，$C$ 分别在 $x$ 轴和 $y$ 轴的正半轴上，顶点 $B$ 的坐标为 $\left(2m,m\right)$，翻折矩形 $OABC$，使点 $A$ 与点 $C$ 重合，得到折痕 $DE$．设点 $B$ 的对应点为 $F$，折痕 $DE$ 所在直线与 $y$ 轴相交于点 $G$，经过点 $C,F,D$ 的抛物线为 $y=ax^2+bx+c$．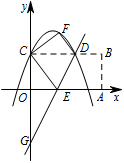
【难度】
【出处】
无
【标注】
  • 题型
    >
    几何部分
    >
    几何变换
    >
    轴对称
  • 题型
    >
    几何部分
    >
    几何变换
    >
    轴对称
  • 题型
    >
    代几综合
    >
    函数与线段
  1. 求点 $D$ 的坐标（用含 $m$ 的式子表示）；
    标注
    • 题型
      >
      几何部分
      >
      几何变换
      >
      轴对称
    答案
    $\left(\dfrac 54m,m\right)$
    解析
    设 $D$ 的坐标为 $\left(d,m\right)$．根据题意得 $CD=d$，$OC=m$．
    因为 $CD \parallel EA$，
    所以 $\angle CDE=\angle AED$．
    由翻折可得 $\angle AED=\angle CED$，
    所以 $\angle CDE=\angle CED$，
    所以 $EA=CE=CD=d$，$OE=2m-d$．
    在 $\mathrm {Rt}\triangle COE$ 中，$OC^2+OE^2=CE^2$，
    即 $m^2+\left(2m-d\right)^2=d^2$，解得 $d=\dfrac 54m$．
    所以 $D$ 的坐标为 $\left(\dfrac 54m,m\right)$．
  2. 若点 $G$ 的坐标为 $\left(0,-3\right)$，求该抛物线的解析式；
    标注
    • 题型
      >
      几何部分
      >
      几何变换
      >
      轴对称
    答案
    $y=-\dfrac{5}{6}{x^2}+\dfrac{25}{12}x+2$
    解析
    作 $DH\perp x$ 轴于点 $H$，作 $FI\perp CD$ 于点 $I$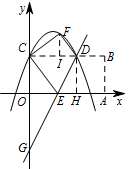．由题意得 $OG=3$，$OE=OA-EA=\dfrac 34m$，$EH=OH-OE=\dfrac 12m$，$DH=m$．
    易证 $\triangle GOE\backsim \triangle DHE$，
    所以 $\dfrac {OE}{HE}=\dfrac {OG}{HD}$，即 $\dfrac {\dfrac 34m}{\dfrac 12m }=\dfrac 3m$．
    解得 $m=2$．
    从而点 $D$ 的坐标为 $\left(\dfrac 52,2\right)$，
    所以 $CD=\dfrac 52$，$CF=2$，$FD=BD=\dfrac 32$．
    而 $CD\cdot FI=CF\cdot FD$，求得 $FI=\dfrac 65$，
    所以 $CI=\sqrt{CF^2-FI^2}=\dfrac 85$，
    所以点 $F$ 的坐标为 $\left(\dfrac 85,\dfrac{16}5\right)$．
    抛物线 $y= a{x^2}+bx+c$ 经过点 $C,D,F$，
    从而有 $\begin{cases}
    c=2,\\
    \dfrac{25}4a+\dfrac 52b+c=2,\\
    \dfrac{64}{25}a+\dfrac 85b+c=\dfrac{16}5,
    \end{cases}$
    解得 $\begin{cases}
    a=-\dfrac{5}{6},\\
    b=\dfrac{25}{12},\\
    c=2.
    \end{cases}$
    所以抛物线解析式为 $y=-\dfrac{5}{6}{x^2}+\dfrac{25}{12}x+2$．
  3. 在第2问的条件下，设线段 $CD$ 的中点为 $M$，在线段 $CD$ 上方的抛物线上是否存在点 $P$，使 $PM=\dfrac{1}{2}EA$？若存在，直接写出 $P$ 的坐标，若不存在，说明理由．
    标注
    • 题型
      >
      代几综合
      >
      函数与线段
    答案
    存在．点 $P$ 坐标为 $\left(\dfrac 85,\dfrac
    {16}5\right)$ 和 $\left(\dfrac 9{10},\dfrac{16}5\right)$
    解析
    由 $PM=\dfrac{1}{2}EA$，可得 $PM=\dfrac{1}{2}CD$．
    所以点 $P$ 在以 $M$ 为圆心，$MC$ 为半径的圆上．
    显然点 $F$ 在 $\odot M$ 上，即点 $F$ 为满足条件的点 $P$ 之一．
    抛物线的对称轴为 $x=\dfrac 54$，
    由抛物线的轴对称性，点 $F\left(\dfrac 85,\dfrac
    {16}5\right)$ 关于直线 $x=\dfrac 54$ 的对称点 $\left(\dfrac 9{10},\dfrac{16}5\right)$ 也为满足条件的点 $P$ 之一．
    综上可得，点 $P$ 坐标为 $\left(\dfrac 85,\dfrac
    {16}5\right)$ 和 $\left(\dfrac 9{10},\dfrac{16}5\right)$．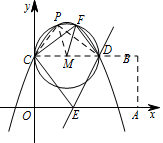
题目 问题1 答案1 解析1 备注1 问题2 答案2 解析2 备注2 问题3 答案3 解析3 备注3
0.121083s