在 $\triangle ABC$ 中，$AB=6$，$AC=BC=5$，将 $\triangle ABC$ 绕点 $A$ 按顺时针方向旋转，得到 $\triangle ADE$，旋转角为 $\alpha$（$0^\circ <\alpha <180^\circ$），点 $B$ 的对应点为点 $D$，点 $C$ 的对应点为点 $E$，连接 $BD,BE$．
【难度】
【出处】
无
【标注】
-
如图，当 $\alpha=60^\circ$ 时，延长 $BE$ 交 $AD$ 于点 $F$，求证：$BF\perp AD$，$AF=DF$．标注答案略解析由旋转的性质可得 $AB=AD$，$AE=DE$，$\angle BAD=\alpha=60^\circ$．
所以 $\triangle ABD$ 为等边三角形，则 $AB=DB$，
从而得到 $BE$ 为 $AD$ 的垂直平分线，
所以 $BF\perp AD$，$AF=DF$． -
在旋转的过程中，过点 $D$ 作 $DG\perp AB$ 于点 $G$，连接 $CE$．当 $\angle DAG=\angle ACB$，且线段 $DG$ 与线段 $AE$ 无公共点时，求 $BE+CE$．标注答案$13$解析如图所示，按照题意画出图形，令 $CE$ 与 $AB$ 的交点为 $H$．
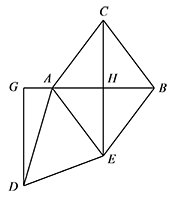由旋转的性质可得 $CA=CB=EA=ED$，$\angle CAB=\angle CBA=\angle EAD=\angle EDA$．
因为 $\angle DAG+\angle DAE+\angle EAB=\angle ACB+\angle CAB+\angle CBA=180^\circ$，且已知 $\angle DAG=\angle ACB$，
所以 $\angle CAB=\angle EAB$．
所以 $AB,CE$ 互相垂直平分，则 $AC=CB=BE=EA$．
所以 $BE+CE=5+2\times \sqrt{5^2-3^2}=13$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
