【难度】
【出处】
无
【标注】
-
【问题提出】
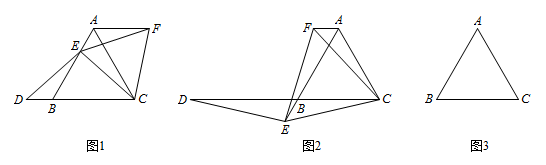
如图 1，已知 $ \triangle ABC $ 是等边三角形，点 $ E $ 在线段 $ AB $ 上，点 $ D $ 在直线 $ BC $ 上，且 $ ED=EC $，将 $ \triangle BCE $ 绕点 $ C $ 顺时针旋转 $60^\circ$ 至 $ \triangle ACF $，连接 $ EF $．试证明：$ AB=DB+AF $．标注答案略解析如图，过点 $E$ 作 $EG\parallel AC$，交 $BC$ 于点 $G$，则 $\triangle EBG$ 为等边三角形．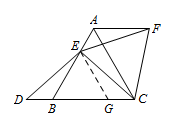
易证 $\triangle EBD\cong \triangle EGC$，
所以 $DB=CG=AE$．
由旋转的性质可得 $AF=BE$，
所以 $AB=BE+AE=AF+DB$． -
【类比探究】
① 如图 2，如果点 $ E $ 在线段 $ AB $ 的延长线上，其它条件不变，线段 $ AB,DB,AF $ 之间又有怎样的数量关系？请说明理由．
② 如果点 $ E $ 在线段 $ BA $ 的延长线上，其他条件不变，请在图 3 的基础上将图形补充完整，并写出 $ AB,DB,AF $ 之间数量关系，不必说明理由．标注答案① $AB=DB-AF$．
② 如图所示：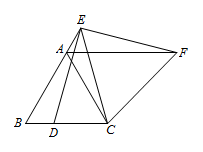
$AF=BD+AB$（或 $AB=AF-BD$）解析① 如图，过点 $E$ 作 $EG\parallel AC$，交 $CD$ 于点 $G$，则 $\triangle EBG$ 为等边三角形．
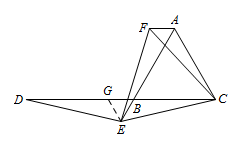易证 $\triangle EGD\cong \triangle EBC$，
所以 $DG=CB=AB$．
由旋转的性质可得 $AF=BE=BG$，
所以 $AB=DG=DB-BG=DB-AF$．
② 如图，过点 $E$ 作 $EG\parallel AC$，交 $BC$ 延长线于点 $G$，则 $\triangle EBG$ 为等边三角形．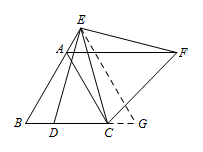
易证 $\triangle EBD\cong \triangle EGC$，
所以 $DB=CG=AE$．
由旋转的性质可得 $AF=BE$，
所以 $AB=BE-AE=AF-DB$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
