$\triangle ABC$ 是等边三角形，以点 $C$ 为旋转中心，将线段 $CA$ 按顺时针方向旋转 $60^\circ$ 得到线段 $CD$，连接 $BD$ 交 $AC$ 于点 $O$．
【难度】
【出处】
无
【标注】
-
如图1，点 $M$ 在 $BC$ 的延长线上，点 $N$ 在线段 $CO$ 上，且 $ND=NM$，连接 $BN$，判断 $\triangle MND$ 的形状，并加以证明；标注答案$\triangle MND$ 为等边三角形解析由旋转的性质可得 $\angle ACD=60^\circ=\angle ACB$，$CD=CA=CB$，
所以 $AC$ 为 $BD$ 的垂直平分线，$\angle CBD=30^\circ$．
所以 $NB=ND=NM$，
从而点 $B,D,M$ 在以 $N$ 为圆心，$NB$ 长为半径的 $\odot N$ 上（如图）．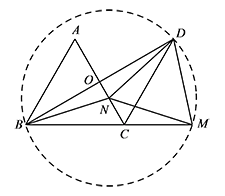
所以 $\angle DNM=2\angle DBM=60^\circ$，
即 $\triangle MND$ 为等边三角形． -
如图2，点 $M$ 在 $BC$ 的延长线上，点 $N$ 在线段 $AO$ 上，且 $ND=NM$，补全图2．求证：$NA=MC$．标注答案补全图形如下
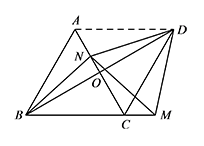解析连接 $AD$．
同理可证 $\triangle MND$ 为等边三角形．
由旋转的性质可得 $\triangle ACD$ 也为等边三角形，
所以易证 $\triangle DAN\cong \triangle DCM$，
从而 $NA=MC$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
