在平面直角坐标系 $xOy$ 中，对于线段 $MN$ 的“三等分变换”，给出如下定义：如图，点 $P,Q$ 为线段 $MN$ 的三等分点，即 $MP=PQ=QN$，将线段 $PM$ 以点 $P$ 为旋转中心顺时针旋转 $90^\circ$ 得到 $PM'$，将线段 $QN$ 以点 $Q$ 为旋转中心顺时针旋转 $90^\circ$ 得到 $QN'$，则称线段 $MN$ 进行了三等分变换，其中 $M',N'$ 记为点 $M,N$ 三等分变换的对应点．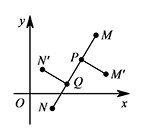
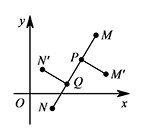
【难度】
【出处】
无
【标注】
-
若点 $P$ 的坐标为 $(2,0)$，点 $Q$ 的坐标为 $(4,0)$，直接写出点 $M'$ 与点 $N'$ 的坐标；标注答案$M'(2,2)$，$N'(4,-2)$解析由已知可得点 $Q$ 绕着点 $P$ 逆时针旋转 $90^\circ$ 可得到点 $M'$，点 $P$ 绕着点 $Q$ 逆时针旋转 $90^\circ$ 可得到点 $N'$，如图所示．
-
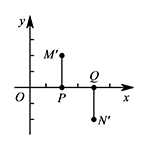
若点 $Q$ 的坐标是 $\left(0,-\dfrac{\sqrt 2}2\right)$，点 $P$ 在 $x$ 轴正半轴上，点 $N'$ 在第二象限，当线段 $PQ$ 的长度为符合条件的最小整数时，求 $OP$ 的长；标注答案$OP=\sqrt{PQ^2-OQ^2}=\dfrac{\sqrt{14}}2$解析如图，过点 $N'$ 作 $N'R\perp y$ 轴于点 $R$．
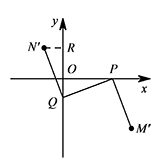易证 $\triangle N'RQ\cong \triangle QOP$，
所以 $OP=RQ>OQ$，即 $OP>\dfrac{\sqrt 2}2$．
而 $PQ^2=OQ^2+OP^2>\dfrac 12+\dfrac 12=1$，
所以线段 $PQ$ 的长度符合条件的最小整数值为 $2$，
从而 $OP=\sqrt{PQ^2-OQ^2}=\dfrac{\sqrt{14}}2$． -
若点 $Q$ 的坐标为 $(0,0)$，点 $M'$ 的坐标为 $(-3,-3)$，直接写出点 $P$ 与点 $N$ 的坐标；标注答案$P(0,-3)$，$N(0,3)$解析如图所示．
-
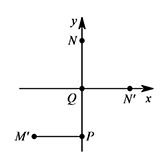
点 $P$ 是以原点 $O$ 为圆心，$1$ 为半径的圆上的一个定点，点 $P$ 的坐标为 $\left(\dfrac{\sqrt 3}2,-\dfrac 12\right)$，当点 $N'$ 在圆 $O$ 内部或圆上时，求线段 $PQ$ 的取值范围及 $PQ$ 取最大值时点 $M'$ 的坐标．标注答案点 $M'$ 的坐标为 $\left(\dfrac{2\sqrt 3-1}2,-\dfrac{\sqrt 3+2}2\right)$解析连接 $PN'$，显然 $\triangle PQN'$ 为等腰直角三角形，
所以 $PQ=\dfrac{\sqrt 2}2PN'$，
显然当 $PN'$ 为 $\odot O$ 的直径时，$PQ$ 取最大值 $\sqrt 2$．
如图，分别过点 $P,Q$ 作 $x$ 轴的垂线，垂足为点 $S,T$．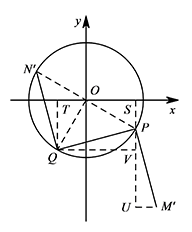
则 $\triangle PSO\cong \triangle OTQ$，
所以 $OT=PS=\dfrac 12$，$QT=OS=\dfrac{\sqrt 3}2$．
分别过点 $M',Q$ 作直线 $PS$ 的垂线，垂足为点 $U,V$．
则 $\triangle M'UP\cong \triangle PVQ$，
所以 $M'U=PV=\dfrac{\sqrt 3-1}2$，$PU=QV=\dfrac{\sqrt 3+1}2$．
所以此时点 $M'\left(\dfrac{2\sqrt 3-1}2,-\dfrac{\sqrt 3+2}2\right)$．
综上可得，线段 $PQ$ 的取值范围为 $0<PQ\leqslant \sqrt 2$，$PQ$ 取最大值时点 $M'$ 的坐标为 $\left(\dfrac{2\sqrt 3-1}2,-\dfrac{\sqrt 3+2}2\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
问题4
答案4
解析4
备注4
