如图,在 $\triangle ABC$ 中,$AB=AC$,点 $E$ 在边 $BC$ 上移动(点 $E$ 不与点 $B,C$ 重合),满足 $\angle DEF=\angle B$,且点 $D,F$ 分别在边 $AB,AC$ 上.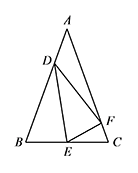
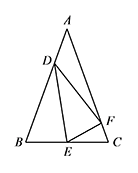
【难度】
【出处】
无
【标注】
-
求证:$\triangle BDE\backsim \triangle CEF$;标注答案略解析由题意可得 $\angle B=\angle DEF=\angle C$.
而 $\angle B+\angle BDE+\angle BED=\angle BED+\angle DEF+\angle CEF=180^\circ$,
所以 $\angle BDE=\angle CEF$,
从而 $\triangle BDE\backsim \triangle CEF$. -
当点 $E$ 移动到 $BC$ 的中点时,求证:$FE$ 平分 $\angle DFC$.标注答案略解析由 $\triangle BDE\backsim \triangle CEF$,
可得 $\dfrac{BE}{CF}=\dfrac{DE}{EF}$.
而 $BE=CE$,
所以 $\dfrac{CE}{CF}=\dfrac{DE}{EF}$,
从而 $\triangle DEF\backsim \triangle ECF$,
所以 $\angle DFE=\angle EFC$,
即 $FE$ 平分 $\angle DFC$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2