如图,在等腰三角形 $ABC$ 中,$\angle BAC=120^\circ$,$AB=AC=2$,点 $D$ 是 $BC$ 边上的一个动点(不与 $B,C$ 重合),在 $AC$ 上取一点 $E$,使 $\angle ADE=30^\circ$,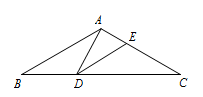

【难度】
【出处】
无
【标注】
-
设 $BD=x,AE=y$,求 $y$ 关于 $x$ 的函数关系式并写出自变量 $x$ 的取值范围;标注答案$y=\dfrac 12x^2-\sqrt 3x+2$($0<x<2\sqrt 3$)解析因为在等腰三角形 $ABC$ 中,$\angle BAC=120^\circ$,
所以 $\angle ABD=\angle ACB=30^\circ$,
所以 $\angle ABD=\angle ADE$,
因为 $\angle ADC=\angle ADE+\angle EDC=\angle ABD+\angle DAB$,
所以 $\angle EDC=\angle DAB$,
所以 $\triangle ABD\backsim \triangle DCE$,
根据题意可得 $BC=2\sqrt 3$,
设 $BD=x,AE=y$,
则 $DC=2\sqrt 3-x,EC=2-y$,
因为 $\dfrac{AB}{BD}=\dfrac{DC}{CE}$,即 $\dfrac{2}{x}=\dfrac{2\sqrt 3-x}{2-y}$,
所以 $y=\dfrac 12x^2-\sqrt 3x+2$($0<x<2\sqrt 3$). -
当 $\triangle ADE$ 是等腰三角形时,求 $AE$ 的长.标注答案当 $\triangle ADE$ 是等腰三角形时,$AE=4-2\sqrt 3$ 或 $AE=\dfrac 23$解析当 $AD=DE$ 时,
此时 $\triangle ABD\cong \triangle DCE$.
则 $AB=CD$,即 $2=2\sqrt 3-x$,
$x=2\sqrt 3-2$,代入 $y=\dfrac 12x^2-\sqrt 3x+2$,
解得 $y=4-2\sqrt 3$,$AE=4-2\sqrt 3$.
当 $AE=ED$ 时,
$\angle EAD=\angle EDA=30^\circ$,$\angle AED=120^\circ$.
所以 $\angle DEC=60^\circ$,$\angle EDC=90^\circ$.
则 $ED=\dfrac 12 EC$,即 $y=\dfrac 12(2-y)$,
解得 $y=\dfrac 23$,即 $AE=\dfrac 23$.
当 $AD=AE$ 时,
$\angle AED=\angle EDA=30^\circ$,$\angle EAD=120^\circ$,
此时点 $D$ 和点 $B$ 重合,与题目不符,此情况不存在,
所以当 $\triangle ADE$ 是等腰三角形时,$AE=4-2\sqrt 3$ 或 $AE=\dfrac 23$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2