如图，等边 $\triangle ABC$ 中，点 $D,E$ 在 $AB,BC$ 上，$AD=2BE=6$，将 $DE$ 绕点 $E$ 顺时针旋转 $60^\circ$，得到 $EF$，取 $EF$ 的中点 $G$，连接 $AG$，延长 $CF$ 交 $AG$ 于点 $H$，若 $2AH=5HG$，求 $BD$ 的长．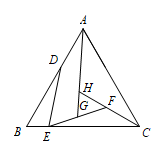
【难度】
【出处】
无
【标注】
【答案】
$BD=9$
【解析】
过点 $F$ 作 $FI\parallel AC$ 交 $BC$ 于点 $I$．
易证 $\triangle DBE\cong \triangle EIF$，
则 $IF=BE,IE=BD$，所以 $IC=IF$，
则 $\angle ACH=\angle BCH=30^\circ$．
延长 $CH$ 交 $AB$ 于点 $J$．
则 $CJ\perp AB,AJ=BJ$．
分别过点 $G,E$ 作 $AB$ 的垂线段，垂足为 $K,L$，
则 $KL=KJ,\dfrac{AJ}{JK}=\dfrac 52,$
所以 $AJ:JK:KL:BL=5:2:2:1$．
因为 $BE=3$，$\angle LEB=30^\circ$，
所以 $BL=1.5,AB=15$，所以 $BD=9$．
易证 $\triangle DBE\cong \triangle EIF$，
则 $IF=BE,IE=BD$，所以 $IC=IF$，
则 $\angle ACH=\angle BCH=30^\circ$．
延长 $CH$ 交 $AB$ 于点 $J$．
则 $CJ\perp AB,AJ=BJ$．
分别过点 $G,E$ 作 $AB$ 的垂线段，垂足为 $K,L$，
则 $KL=KJ,\dfrac{AJ}{JK}=\dfrac 52,$所以 $AJ:JK:KL:BL=5:2:2:1$．
因为 $BE=3$，$\angle LEB=30^\circ$，
所以 $BL=1.5,AB=15$，所以 $BD=9$．
答案
解析
备注
