如图，边长为 $2\sqrt 2$ 的正方形 $ABCD$ 中，$P$ 是对角线 $AC$ 上的一个动点（点 $P$ 与 $A,C$ 不重合），连接 $BP$，将 $BP$ 绕点 $B$ 顺时针旋转 $90^\circ$ 到 $BQ$．连接 $QP$，$QP$ 与 $BC$ 交于点 $E$．$QP$ 延长线与 $AD$（或 $AD$ 延长线）交于点 $F$．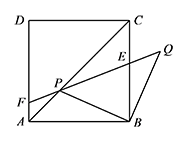
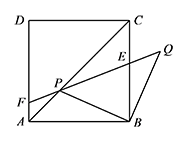
【难度】
【出处】
无
【标注】
-
设 $AP=x,CE=y$，试写出 $y$ 关于 $x$ 的函数关系式；标注答案$y=-\dfrac{\sqrt 2}4x^2+\sqrt 2x$解析由题意可得 $\triangle PBQ$ 为等腰直角三角形，
所以 $\angle BPQ=45^\circ=\angle ACB=\angle CAB$．
由“一线三等角模型”可得 $\triangle ABP\backsim \triangle CPE$，
从而 $\dfrac{AP}{CE}=\dfrac{AB}{CP}$，
所以 $\dfrac{x}{y}=\dfrac{2\sqrt 2}{4-x}$，即 $y=-\dfrac{\sqrt 2}4x^2+\sqrt 2x$． -
猜想 $PF$ 与 $EQ$ 的数量关系，并证明你的结论．标注答案$EQ=PF$解析如图，过点 $P$ 作 $PG\perp PF$ 交 $AB$ 于点 $G$．
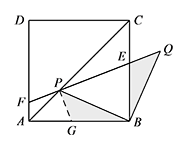由“对角互补模型”可得 $PF=PG$．
因为 $\angle PBQ=\angle ABC=90^\circ$，
所以 $\angle PBG=\angle QBE$．
而 $\angle GPB=\angle GPQ-\angle BPQ=45^\circ=\angle Q$，
又 $BP=BQ$，
所以 $\triangle PBG\cong \triangle QBE$，
从而 $EQ=GP=PF$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
