如图，已知 $PA,PB$ 是由 $\odot O$ 外一点 $P$ 引出的两条切线，$M,N$ 分别是线段 $AP,AB$ 的中点，直线 $MN$ 交 $\odot O$ 于 $C,E$ 两点，点 $N$ 在 $M$ 与 $C$ 之间，$PC$ 交 $\odot O$ 于点 $D$，延长 $ND$ 交 $PB$ 于点 $Q$，证明：四边形 $MNQP$ 为菱形．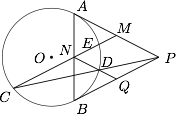
【难度】
【出处】
2012年全国高中数学联赛辽宁省预赛
【标注】
【答案】
略
【解析】
连接 $OP,OA,OC,EP$，如图．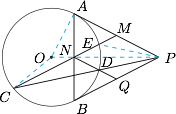
显然 $O,P,N$ 三点共线，且 $OP\perp AB$．
因为 $M$ 是 $PA$ 的中点，$N$ 是 $AB$ 的中点，所以$$MN=MP=MA,MN\parallel PB,$$因此$$PM^2=AM^2=ME\cdot MC,$$所以 $\triangle MPE\backsim \triangle MCP$，故 $\angle MCP=\angle MPE$．
又 $O,A,P,B$ 四点共圆，所以$$ON\cdot PN=AN\cdot BN=CN\cdot EN,$$故 $O,C,P,E$ 四点共圆，从而$$\angle OCN=\angle EPN.$$又 $\triangle PAO$ 是直角三角形，有$$PN\cdot PO=PA^2=PD\cdot PC,$$于是 $C,D,N,O$ 四点共圆，所以$$\angle QNP=\angle PCO=\angle MCP+\angle MCO=\angle MPE+\angle EPN=\angle APN,$$故 $PM\parallel NQ$，四边形 $MNQP$ 是菱形．
显然 $O,P,N$ 三点共线，且 $OP\perp AB$．因为 $M$ 是 $PA$ 的中点，$N$ 是 $AB$ 的中点，所以$$MN=MP=MA,MN\parallel PB,$$因此$$PM^2=AM^2=ME\cdot MC,$$所以 $\triangle MPE\backsim \triangle MCP$，故 $\angle MCP=\angle MPE$．
又 $O,A,P,B$ 四点共圆，所以$$ON\cdot PN=AN\cdot BN=CN\cdot EN,$$故 $O,C,P,E$ 四点共圆，从而$$\angle OCN=\angle EPN.$$又 $\triangle PAO$ 是直角三角形，有$$PN\cdot PO=PA^2=PD\cdot PC,$$于是 $C,D,N,O$ 四点共圆，所以$$\angle QNP=\angle PCO=\angle MCP+\angle MCO=\angle MPE+\angle EPN=\angle APN,$$故 $PM\parallel NQ$，四边形 $MNQP$ 是菱形．
答案
解析
备注
