正方形 $ABCD$ 的边长为 $1$，点 $O$ 是 $BC$ 边上的一个动点（与 $B,C$ 不重合），以 $O$ 为顶点在 $BC$ 所在直线的上方作 $\angle MON=90^\circ$．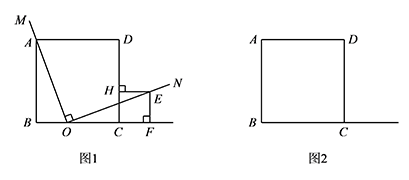
【难度】
【出处】
无
【标注】
-
如图1，在 $ON$ 上截取 $OE=OA$，过 $E$ 点作 $EF$ 垂直于直线 $BC$，垂足为点 $F$，$EH\perp CD$ 于点 $H$，求证：四边形 $EFCH$ 为正方形．标注答案略解析由题意可得 $\angle AOB+\angle FOE=\angle AOB+\angle BAO=90^\circ$，
所以 $\angle FOE=\angle BAO$．
而 $\angle ABO=\angle OFE=90^\circ$，$OA=OE$，
所以 $\triangle ABO\cong \triangle OFE$，
所以 $BO=FE$，$BC=AB=OF$．
从而 $CF=BO=FE$．
显然四边形 $EFCH$ 为矩形，
所以四边形 $EFCH$ 为正方形． -
当 $OM$ 不过 $A$ 点时，设 $OM$ 交边 $AB$ 于点 $G$，且 $OG=1$．在 $ON$ 上存在点 $P$，过 $P$ 点作 $PK$ 垂直于直线 $BC$，垂足为点 $K$，使得 $S_{\triangle PKO}=4S_{\triangle OBG}$，连接 $GP$，求四边形 $PKBG$ 的最大面积．标注答案四边形 $PKBG$ 的最大面积为 $\dfrac 94$解析按题意画出图形．
易证 $\triangle GBO\backsim \triangle OKP$，
所以 $\dfrac{OP}{OG}=\sqrt{\dfrac{S_{\triangle PKO}}{S_{\triangle OBG}}}=\sqrt 4=2$，即 $OP=2OG=2$，
从而 $S_{\triangle GOP}=\dfrac 12 OG\cdot OP=1$．
由 $S_{\text{四边形}PDBG}=S_{\triangle PKO}+S_{\triangle GBO}+S_{\triangle GOP}=5S_{\triangle GBO}+1$，
所以当 $S_{\triangle GBO}$ 最大时，$S_{\text{四边形}PDBG}$ 取最大值．
设 $BG=m$，$BO=n$，则 $m^2+n^2=1$．
而 $(m-n)^2\geqslant 0$，即 $m^2+n^2\geqslant 2mn$．
所以 $S_{\triangle GBO}=\dfrac 12mn\leqslant \dfrac 14$，
从而 $S_{\text{四边形}PDBG}=5S_{\triangle GBO}+1\leqslant \dfrac 94$，
即四边形 $PKBG$ 的最大面积为 $\dfrac 94$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
