查看数据源：5912bf41e020e700094b0d93
正方形 $ABCD$ 边长为 $1$，现对折该正方形，使得 $D$ 始终落在线段 $AB$ 上，求折痕上的点所构成的点集的面积．
【难度】
【出处】
2009年中国科学技术大学自主招生保送生测试
【标注】
  • 知识点
    >
    解析几何
    >
    抛物线
    >
    抛物线的定义
  • 知识点
    >
    微积分初步
    >
    积分
    >
    定积分的几何意义
【答案】
略
【解析】
如图，若 $P$ 是折痕上的点，则在 $AB$ 上存在一点 $M$，使得 $PD = PM$，所以 $PD \geqslant PH$（$P$ 到 $AB$ 上的垂线），且 $PD \leqslant \max \left\{ {PA,PB} \right\}$．反之也成立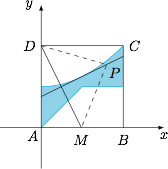．建立直角坐标系如图，设 $P\left( {x, y} \right)$，则$$\begin{cases}
\sqrt {{x^2} + {{(y - 1)}^2}} \geqslant y \\
\sqrt {{x^2} + {{(y - 1)}^2}} \leqslant \sqrt {{{(x - 1)}^2} + {y^2}} , &0 \leqslant x \leqslant \dfrac{1}{2},\end{cases}$$或$$\begin{cases}\sqrt {{x^2} + {{(y - 1)}^2}} \geqslant y \\
\sqrt {{x^2} + {{(y - 1)}^2}} \leqslant \sqrt {{x^2} + {y^2}} ,& \dfrac{1}{2} \leqslant x \leqslant 1\end{cases}$$化简可得$$\begin{cases}
y \leqslant \dfrac{{{x^2}}}{2} + \dfrac{1}{2},&0 \leqslant x \leqslant 1\\
y \geqslant x, &0 \leqslant x \leqslant \dfrac{1}{2},\end{cases}$$或$$\begin{cases}y \leqslant \dfrac{{{x^2}}}{2} + \dfrac{1}{2},&0 \leqslant x \leqslant 1\\
y \geqslant \dfrac{1}{2},&\dfrac{1}{2} \leqslant x \leqslant 1.\end{cases}$$要求如图阴影所示的面积，
易算出为$$\int_0^1 {\left[ {\left( {\dfrac{{{x^2}}}{2} + \dfrac{1}{2}} \right) - \dfrac{1}{2}} \right]} {\rm d}x + \dfrac{1}{2} \times \dfrac{1}{2} \times \dfrac{1}{2} = \dfrac{7}{{24}}.$$
答案 解析 备注
0.109124s