某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究，提出下列问题，请你给出证明．
【难度】
【出处】
无
【标注】
-
如图1，矩形 $ABCD$ 中，$EF\perp GH$，$EF$ 分别交 $AB$，$CD$ 于点 $E$，$F$，$GH$ 分别交 $AD$，$BC$ 于点 $G$，$H$．求证：$\dfrac{EF}{GH} =\dfrac{AD}{AB}$；
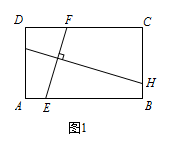标注答案略解析过点 $A$ 作 $AP\parallel EF$，交 $CD$ 于 $P$，过点 $B$ 作 $BQ\parallel GH$，交 $AD$ 于 $Q$，如图1，
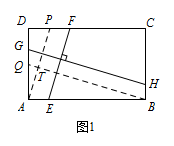因为四边形 $ABCD$ 是矩形，
所以 $AB\parallel DC$，$AD\parallel BC$．
所以四边形 $AEFP$，四边形 $BHGQ$ 都是平行四边形，
所以 $AP=EF$，$GH=BQ$．
又因为 $GH\perp EF$，
所以 $AP\perp BQ$，
所以 $\angle QAT+\angle AQT=90^\circ $．
因为四边形 $ABCD$ 是矩形，
所以 $\angle DAB=\angle D=90^\circ $，
所以 $\angle DAP+\angle DPA=90^\circ $，
所以 $\angle AQT=\angle DPA$．
所以 $\triangle PDA\backsim \triangle QAB$，
所以 $\dfrac{AP}{BQ}=\dfrac{AD}{AB}$，
所以 $\dfrac{EF}{GH}=\dfrac{AD}{AB}$． -
如图2，在满足（$1$）的条件下，又 $AM\perp BN$，点 $M$，$N$ 分别在边 $BC$，$CD$ 上，若 $\dfrac{EF}{GH}=\dfrac{11}{15}$，则 $\dfrac{BN}{AM}$ 的值为；
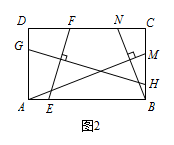标注答案$\dfrac{11}{15}$解析如图2，
因为 $EF\perp GH$，$AM\perp BN$，
所以由（$1$）中的结论可得 $\dfrac{EF}{GH}=\dfrac{AD}{AB}$，$\dfrac{BN}{AM} =\dfrac{AD}{AB}$，
所以 $\dfrac{BN}{AM}=\dfrac{EF}{GH}=\dfrac{11}{15}$． -
如图3，四边形 $ABCD$ 中，$\angle ABC=90^\circ $，$AB=AD=10$，$BC=CD=5$，$AM\perp DN$，点 $M$，$N$ 分别在边 $BC$，$AB$ 上，求 $\dfrac{DN}{AM}$ 的值．
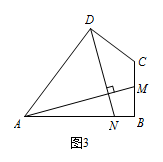标注答案$\dfrac{DN}{AM}=\dfrac{4}{5}$解析过点 $D$ 作平行于 $AB$ 的直线，交过点 $A$ 平行于 $BC$ 的直线于 $R$，交 $BC$ 的延长线于 $S$，如图3，
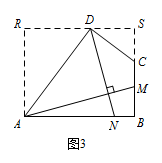则四边形 $ABSR$ 是平行四边形．
因为 $\angle ABC=90^\circ $，
所以四边形 $ABSR$ 是矩形，
所以 $\angle R=\angle S=90^\circ$，$RS=AB=10$，$AR=BS$．
因为 $AM\perp DN$，
所以由（$1$）中的结论可得 $\dfrac{DN}{AM}=\dfrac{AR}{AB}$．
设 $SC=x$，$DS=y$，则 $AR=BS=5+x$，$RD=10-y$，
所以在 $\mathrm {Rt}\triangle CSD$ 中，$x^2+y^2=25$ ①，
在 $\mathrm {Rt}\triangle ARD$ 中，$\left(5+x\right)^2+\left(10-y\right)^2=100$ ②，
由 ② $-$ ① 得 $x=2y-5$ ③，
解方程组 $ \begin{cases}x^2+y^2=25,\\x=2y-5.\end{cases} $
得 $ \begin{cases}x=-5,\\y=0.\end{cases} $（舍去），或 $ \begin{cases}x=3,\\y=4.\end{cases} $
所以 $AR=5+x=8$，
所以 $\dfrac{DN}{AM}=\dfrac{AR}{AB}=\dfrac{8}{10}=\dfrac{4}{5}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
