如图，已知正方形 $ABCD$ 的边长为 $4$，点 $P$ 是 $AB$ 边上的一个动点，连接 $CP$，过点 $P$ 作 $PC$ 的垂线交 $AD$ 于点 $E$，以 $PE$ 为边作正方形 $PEFG$，顶点 $G$ 在线段 $PC$ 上，对角线 $EG,PF$ 相交于点 $O$．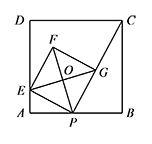
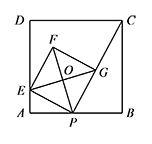
【难度】
【出处】
无
【标注】
-
若 $AP=1$，则 $AE=$
所以 $\dfrac{EA}{PB}=\dfrac{PA}{CB}$，
所以 $AE=\dfrac 34$． -
当点 $P$ 从点 $A$ 运动到点 $B$ 时，点 $O$ 也随之运动，求点 $O$ 经过的路径长；标注答案点 $O$ 经过的路径长为 $\dfrac 12AC=2\sqrt 2$解析如图，过点 $G$ 作 $GH\perp AB$ 于点 $G$．
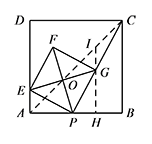易证 $\triangle EAP\cong \triangle PHG$，
所以 $EA=PH$，$AP=HG$．
连接 $AO$ 并延长，交 $HG$ 的延长线于点 $I$，
则 $\triangle AOE\cong \triangle IOG$，
所以 $GI=EA=PH$，从而 $HI=HA$，
所以 $\angle IAH=45^\circ$．
即点 $O$ 在对角线 $AC$ 上，
所以点 $O$ 经过的路径长为 $\dfrac 12AC=2\sqrt 2$． -
在点 $P$ 从点 $A$ 到点 $B$ 的运动过程中，$\triangle APE$ 的外接圆的圆心也随之运动，求该圆心到 $AB$ 边的距离的最大值．标注答案$\dfrac 12$解析由 $\triangle EAP\backsim \triangle PBC$，可得 $\dfrac{EA}{PB}=\dfrac{PA}{CB}$．
令 $PB=x$，则 $AP=4-x$，
所以 $\dfrac{AE}{x}=\dfrac{4-x}{4}$，即 $AE=-\dfrac 14(x-2)^2+1$．
所以当 $x=2$，即 $PB=2$ 时，$AE$ 取最大值 $1$．
$\triangle APE$ 的外接圆为以 $EP$ 为直径的 $\odot M$，其圆心为 $EP$ 的中点 $M$．
如图，过点 $M$ 作 $MN\perp AB$ 于点 $N$．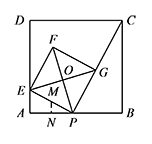
则 $MN=\dfrac 12AE$，
所以 $MN$ 的最大值为 $\dfrac 12$，
即 $\triangle APE$ 的外接圆的圆心到 $AB$ 边的距离的最大值为 $\dfrac 12$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
