如图，在正方形 $ABCD$ 中，点 $P$ 在 $AD$ 上，且不与 $A$，$D$ 重合，$BP$ 的垂直平分线分别交 $CD$，$AB$ 于 $E$，$F$ 两点，垂足为 $Q$，过 $E$ 作 $EH\perp AB$ 于 $H$．求证：$HF=AP$．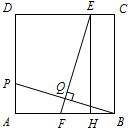
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
设 $EH$ 与 $BP$ 交于 $M$ 点．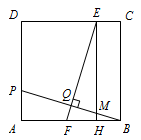
因为 $ EQ\perp BP$，$EH\perp AB$，
所以 $ \angle EQM=\angle BHM=90^\circ $．
又 $\angle EMQ=\angle BMH$，
所以 $ \angle QEM=\angle HBM$．
因为四边形 $ABCD$ 为正方形，
所以 $ AB=BC$，$\angle C=\angle CBA=90^\circ$，
又 $\angle BHM=90^\circ$，
所以四边形 $EHBC$ 为矩形，
所以 $EH=BC$，
所以 $ EH=AB$，
在 $\mathrm {Rt}\triangle APB$ 与 $\mathrm {Rt}\triangle HFE$ 中
$\begin{cases}∠PAB=∠FHE,\\
AB=EH,\\ \angle PBA=\angle FEH,\end{cases}$
所以 $ \triangle PAB\cong \triangle FHE$（${\mathrm {ASA}}$）
所以 $ HF=AP$．
因为 $ EQ\perp BP$，$EH\perp AB$，所以 $ \angle EQM=\angle BHM=90^\circ $．
又 $\angle EMQ=\angle BMH$，
所以 $ \angle QEM=\angle HBM$．
因为四边形 $ABCD$ 为正方形，
所以 $ AB=BC$，$\angle C=\angle CBA=90^\circ$，
又 $\angle BHM=90^\circ$，
所以四边形 $EHBC$ 为矩形，
所以 $EH=BC$，
所以 $ EH=AB$，
在 $\mathrm {Rt}\triangle APB$ 与 $\mathrm {Rt}\triangle HFE$ 中
$\begin{cases}∠PAB=∠FHE,\\
AB=EH,\\ \angle PBA=\angle FEH,\end{cases}$
所以 $ \triangle PAB\cong \triangle FHE$（${\mathrm {ASA}}$）
所以 $ HF=AP$．
答案
解析
备注
