在矩形 $ABCD$ 中,已知 $AD > AB$,在边 $AD$ 上取点 $E$,使 $AE = AB$,连接 $CE$,过点 $E$ 作 $EF \perp CE$,与边 $AB$ 或其延长线交于点 $F$.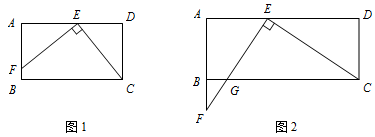
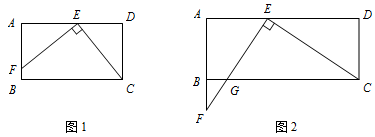
【难度】
【出处】
无
【标注】
-
猜想:如图 1,当点 $F$ 在边 $AB$ 上时,线段 $AF$ 与 $DE$ 的大小关系为
-
探究:如图 2,当点 $F$ 在边 $AB$ 的延长线上时,$EF$ 与边 $BC$ 交于点 $G$.判断线段 $AF$ 与 $DE$ 的大小关系,并加以证明.标注答案$AF=DE$解析
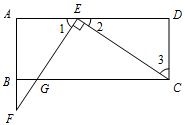 因为 $EF\perp CE$,
因为 $EF\perp CE$,
所以 $ \angle CEF=90^\circ$,
所以 $ \angle 1+\angle 2=90^\circ$.
因为四边形 $ABCD$ 为矩形,
所以 $\angle A=\angle D=90^\circ$,$AB=CD$.
所以 $\angle 2+\angle 3=90^\circ$,
所以 $\angle 1=\angle 3$.
因为 $ AE=AB$,
所以 $ AE=DC$,
所以 $ \triangle AEF\cong\triangle DCE$,
所以 $ AF=DE$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2