在平面直角坐标系 $xOy$ 中，点 $A$ 的坐标为 $(0,m)$，且 $m\ne 0$，点 $B$ 的坐标为 $(n,0)$，将线段 $AB$ 绕点 $B$ 旋转 $90^\circ$，分别得到线段 $BP_1,BP_2$，称点 $P_1,P_2$ 为点 $A$ 关于点 $B$ 的“伴随点”，图1位点 $A$ 关于点 $B$ 的“伴随点”的示意图．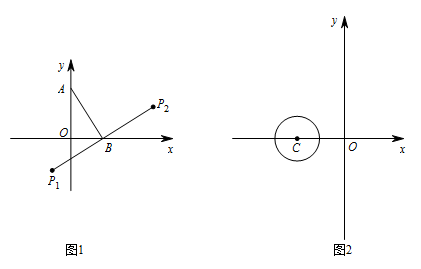
【难度】
【出处】
无
【标注】
-
已知点 $A(0,4)$，点 $(x,y)$ 是点 $A$ 关于点 $B$ 的“伴随点”，求出 $y$ 与 $x$ 之间的关系式；标注答案$y=x-4$解析如图
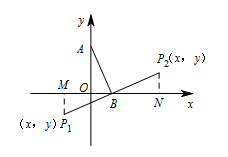过点 $P_1,P_2$ 分别向 $x$ 轴做垂线，垂足分别为 $M,N$，
当 $P_1(x,y)$ 时，因为 $AB=BP_1,\angle ABO=\angle BP_1M$，
所以 $\triangle AOB\cong \triangle BMP_1$，
所以 $BM=OA=4,OB=MP_1=-y$，
所以 $BM=OB+OM=-y-x=4$，即 $y=-x-4$；
当 $P_2(x,y)$ 时，因为 $AB=BP_2,\angle ABO=\angle BP_2N$，
所以 $\triangle AOB\cong \triangle BOP_2$，
所以 $BN=OA=4,OB=NP_2=y$，
所以 $BN=ON-OB=x-y=4$，即 $y=x-4$． -
如图2，点 $C$ 的坐标为 $(-3,0)$，以 $C$ 为圆心，$\sqrt 2$ 为半径作圆，若在 $\odot C$ 上存在点 $A$ 关于点 $B$ 的“伴随点”，求出点 $A$ 纵坐标 $m$ 的取值范围．标注答案$-5\leqslant m\leqslant -1$ 或 $1\leqslant m\leqslant 5$解析若设点 $A(0,m)$，点 $(x,y)$ 是点 $A$ 关于点 $B$ 的“伴随点”，则 $y$ 与 $x$ 之间的关系式为：$y=-x-m,y=x-m$．
因为在 $\odot C$ 上存在点 $A$ 关于点 $B$ 的“伴随点”，
所以 $\odot C$ 与直线 $y=-x-m,y=x-m$ 的位置关系为相交或相切．
如图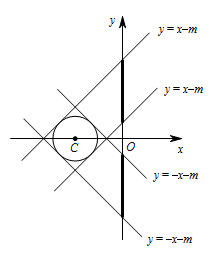
当 $y=x-m$ 与 $\odot O$ 相切时，$m=5,1$．
当 $y=-x-m$ 与 $\odot O$ 相切时，$m=-5,-1$．
所以 $-5\leqslant m\leqslant -1$ 或 $1\leqslant m\leqslant 5$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
