查看数据源：5909925d38b6b4000adaa26f
如图，已知抛物线 $y=\dfrac{\sqrt 2}{8}(x+2)(x-4)$ 与 $x$ 轴交于点 $A,B$（点 $A$ 位于点 $B$ 的左侧），与 $y$ 轴交于点 $C$，$CD\parallel x$ 轴交抛物线于点 $D$．$P$ 是抛物线上一点，是否存在点 $P$，使以 $P,A,B$ 为顶点的三角形与 $\triangle ABD$ 相似（$\triangle PAB$ 与 $\triangle ABD$ 不重合）？若存在，求出点 $P$ 的坐标，若不存在，说明理由．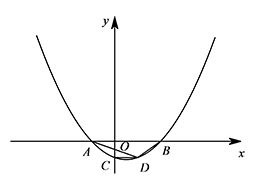
【难度】
【出处】
无
【标注】
  • 题型
    >
    代几综合
    >
    相似三角形的存在性
【答案】
存在，点 $P$ 的坐标为 $(-4,2\sqrt 2),(6,2\sqrt 2)$ 或 $(0,-\sqrt 2)$ 时，以 $P,A,B$ 为顶点的三角形与 $\triangle ABD$ 相似
【解析】
因为 $A(-2,0)$，$B(4,0)$，$C(0,-\sqrt 2)$，
过点 $D(2,-\sqrt 2)$ 作 $DE\perp BA$，垂足为 $E$．
由勾股定理得 $AD=3\sqrt 2$，$BD=\sqrt 6$．
① 如图，当 $\triangle P_1AB\backsim \triangle ADB$ 时，
$\dfrac{P_1B}{AB}=\dfrac{AB}{BD}$，所以 $P_1B=6\sqrt 6$．
过点 $P_1$ 作 $P_1M_1\perp AB$ 垂足为 $M_1$，
所以 $\dfrac{P_1M_1}{P_1B}=\dfrac{DE}{BD}$，解得 $P_1M_1=6\sqrt 2$．
因为 $\dfrac{BM_1}{P_1B}=\dfrac{BE}{BD}$，
所以 $BM_1=12$，
所以点 $P_1$ 的坐标为 $(-8,6\sqrt 2)$，
因为此时点 $P_1$ 不在抛物线上，所以此种情况不存在．
② 当 $\triangle P_2AB\backsim \triangle BDA$ 时，
$\dfrac{P_2B}{AB}=\dfrac{AB}{AD}$，所以 $P_2B=6\sqrt 2$．
过点 $P_2$ 作 $P_2M_2\perp AB$ 垂足为 $M_2$，
所以 $\dfrac{P_2M_2}{P_2B}=\dfrac{DE}{AD}$，解得 $P_2M_2=2\sqrt 2$．
因为 $\dfrac{BM_2}{P_2B}=\dfrac{AE}{AD}$，
所以 $BM_2=8$，
所以点 $P_2$ 的坐标为 $(-4,2\sqrt 2)$，
将 $x=-4$ 代入抛物线的解析式得 $y=2\sqrt 2$，
所以点 $P_2$ 在抛物线上，
③ 由抛物线的对称性可知：点 $P_2$ 与点 $P_3$ 关于直线 $x=1$ 对称，
所以 $P_3$ 的坐标为 $(6,2\sqrt 2)$．
④ 当点 $P_4$ 位于点 $C$ 处时，两个三角形全等，所以点 $P_4$ 的坐标为 $(0,-\sqrt 2)$，
综上所述，点 $P$ 的坐标为 $(-4,2\sqrt 2),(6,2\sqrt 2)$ 或 $(0,-\sqrt 2)$ 时，以 $P,A,B$ 为顶点的三角形与 $\triangle ABD$ 相似．
答案 解析 备注
0.109431s