如图,四边形 $ABCD$ 是圆内接四边形,且 $AB\cdot CD=AD\cdot BC$,$E$ 是对角线 $AC$ 上一点.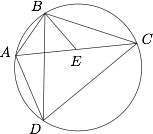

【难度】
【出处】
2012年全国高中数学联赛福建省预赛
【标注】
-
若 $E$ 是 $AC$ 中点,求证:$\angle ABE=\angle DBC$;标注答案略解析由托勒密定理知,$$AC\cdot BD=AB\cdot DC+AD\cdot BC.$$因为$$AB\cdot CD=AD\cdot BC,$$且 $E$ 是 $AC$ 中点,所以$$AB\cdot CD=AD\cdot BC-\dfrac12AC\cdot BD=AE\cdot BD,$$因此$$\dfrac{AB}{AE}=\dfrac{DB}{DC}.$$又 $\angle BAE=\angle BDC$,所以$$\triangle BAE\backsim\triangle BDC,$$因此 $\angle ABE=\angle DBC$.
-
若 $\angle ABE=\angle DBC$,试问 $E$ 是否为 $AC$ 中点?说明理由.标注答案是解析由 $\angle ABE=\angle DBC$ 以及 $\angle BAE=\angle BDC$ 知,$$\triangle BAE\backsim\triangle BDC,$$所以 $\dfrac{AB}{AE}=\dfrac{DB}{DC}$,即$$AB\cdot DC=AE\cdot BD.\qquad\cdots\cdots\text{ ① }$$又由托勒密定理以及 $AB\cdot CD=AD\cdot BC$ 知,$$AB\cdot CD=AD\cdot BC=\dfrac12 AC\cdot BD,\qquad\cdots\cdots\text{ ② }$$由 ①② 得$$AE=\dfrac12AC,$$即 $E$ 为 $AC$ 中点.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2