如图，直线 $y=-x+3$ 与 $x$ 轴，$y$ 轴分别相交于点 $B$，$C$，经过 $B$，$C$ 两点的抛物线 $y=x^2-4x+3$ 与 $x$ 轴的另一个交点为 $A$，顶点为 $P$，且对称轴为直线 $x=2$．连接 $AC$，在 $x$ 轴上是否存在一点 $Q$，使得以点 $P$，$B$，$Q$ 为顶点的三角形与 $\triangle ABC$ 相似，若存在，求出点 $Q$ 的坐标；若不存在，请说明理由．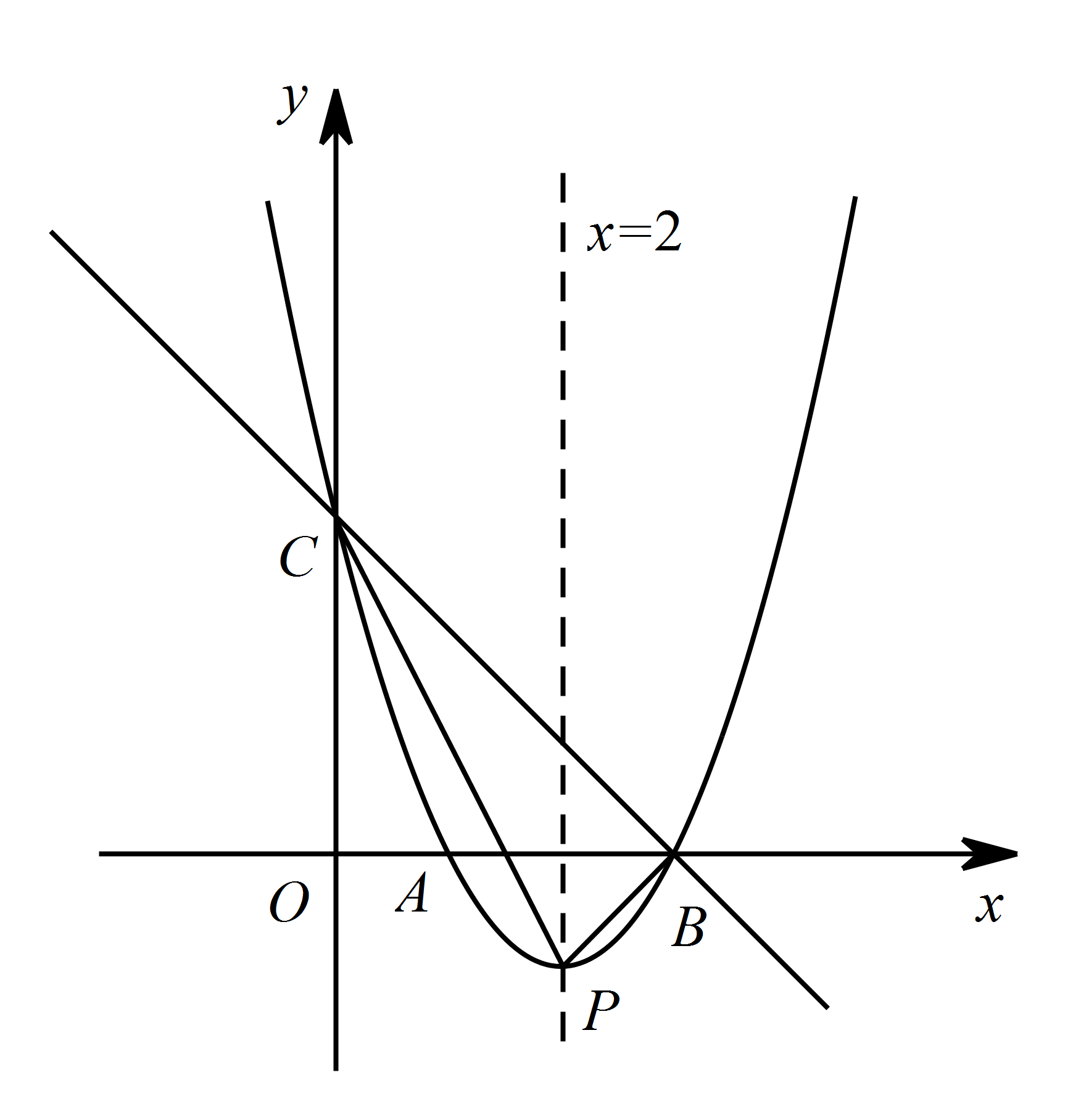
【难度】
【出处】
无
【标注】
【答案】
存在．点 $Q$ 的坐标为 $\left(\dfrac{7}{3 },0\right)$ 或 $\left(0,0\right)$
【解析】
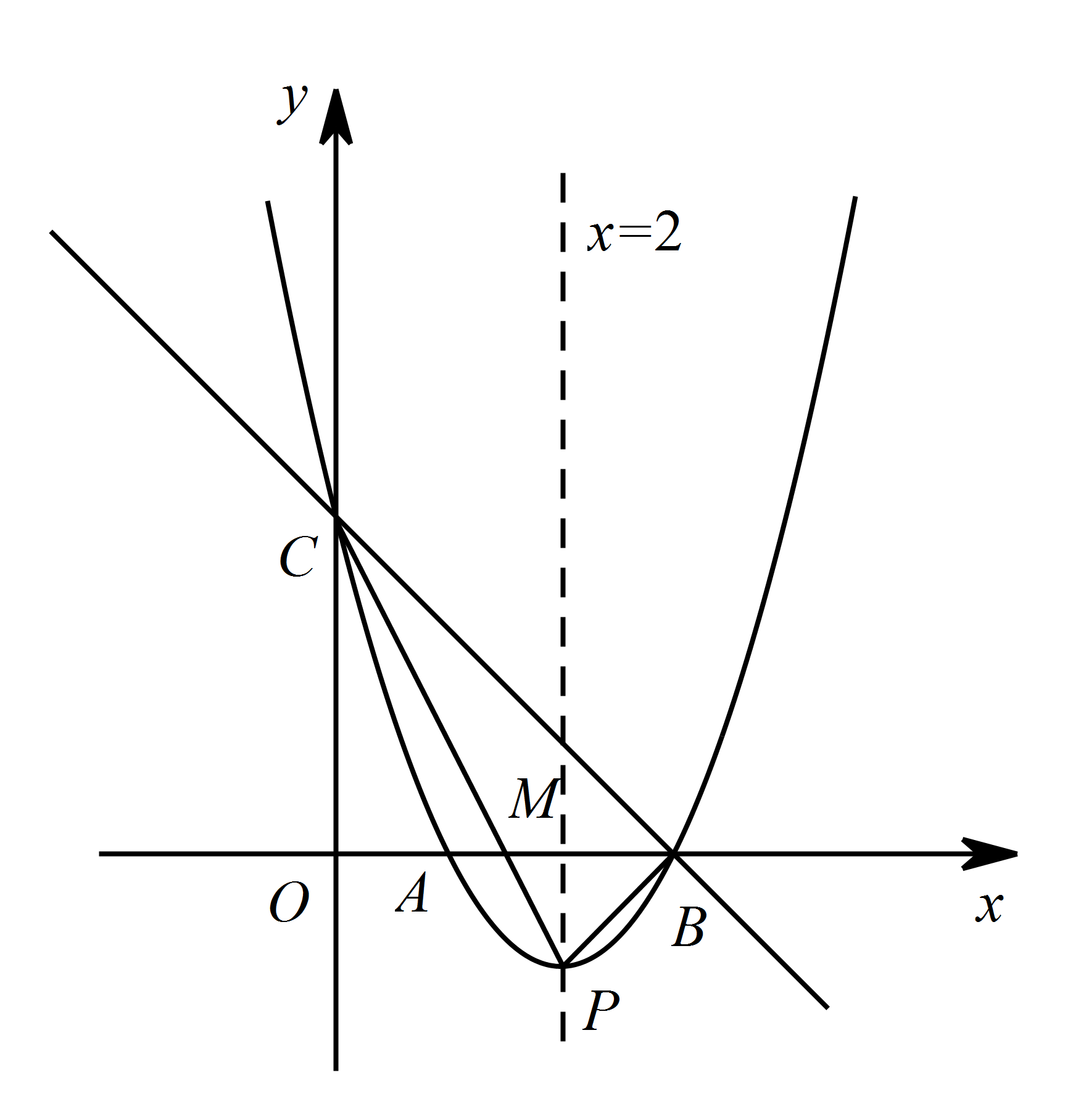设 $Q\left(x,0\right)$，分两种情况讨论：① 当点 $Q$ 在点 $B$ 的左侧时，$QB=3-x$，
因为抛物线对称轴 $x=2$ 与 $x$ 轴的交点为 $M\left(2,0\right)$，又 $P\left(2,-1\right)$，$B\left(3,0\right)$，
所以 $PM=BM=1$，所以 $\triangle PMB$ 是等腰直角三角形，
所以 $\angle QBP=45^\circ$．
因为 $B\left(3,0\right)$，$C\left(0,3\right)$，所以 $\angle ABC=45^\circ$
所以 $\angle ABC=\angle QBP$，
所以当 $\dfrac{QB}{AB }=\dfrac{PB}{CB }$ 或 $\dfrac{QB}{CB }=\dfrac{PA}{AB }$ 时，$\triangle PBA\backsim\triangle ABC$，
i）当 $\dfrac{QB}{AB }=\dfrac{PB}{CB }$ 时，即 $\dfrac{3-x}{2 }=\dfrac{\sqrt{2}}{3\sqrt{2} }$，解得：$x=\dfrac{7}{3 }$，此时 $Q\left(\dfrac{7}{3 },0\right)$．
ii）当 $\dfrac{QB}{CB }=\dfrac{PB}{AB }$ 时，即 $\dfrac{3-x}{3\sqrt{2} }=\dfrac{\sqrt{2}}{2 }$，解得：$x=0$，此时 $Q\left(0,0\right)$．
② 当点 $Q$ 在点 $B$ 的右侧时，
因为 $\angle PBQ=180^\circ-45^\circ=135^\circ$，
所以 $\angle BQP\ne45^\circ$ 或 $\angle BPQ\ne45^\circ$，符合条件的 $\triangle PBQ$ 不存在．
综上所述，点 $Q$ 的坐标为 $\left(\dfrac{7}{3 },0\right)$ 或 $\left(0,0\right)$．
答案
解析
备注
